Деление произвольно заданного угла на 3 равные части.
( Трисекция угла )
Е. И. Терёшкин.Россия. г. Пенза
Чертим две пары пересекающихся прямых, чтобы верхний и нижний вертикальные углы были острыми (чертеж 1) и тупыми (чертеж 2) .
В местах пересечения ставим точки O.

чертёж 1. Верхний и нижний вертикальные углы острые

чертёж 2. Верхний и нижний вертикальные углы тупые
Проводим общие биссектрисы обоих вертикальных острых углов (рисунок 1) и обоих вертикальных тупых углов (рисунок 2). Из точек

любыми радиусами описываем окружности. В местах пересечения сторон нижнего острого угла (рисунок 1) и тупого угла(рисунок 2) с дугами окружностей ставим точки

и

. Далее из точек

параллельно биссектрисам проводим линии вверх до пересечения с продолжениями линий

и дугами окружностей и ставим точки

. На прямых

вправо строим равносторонний треугольник

. Соединяем точки

и

. Проводим биссектрисы углов

до пересечения с прямыми

и ставим точки

. Из точек

радиусами

проводим окружности. В местах пересечения окружностей радиуса

с биссектрисами острых и тупых углов ставим точки

и

. Из точек

параллельно

проводим прямые до пересечения с продолжениями прямых

и ставим точки

. Из точек

параллельно

проводим прямые до пересечения с продолжениями прямых

и ставим точки
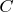
.

- это и есть углы, которые мы будем делить на три равные части. Проведем прямые

. Из точек

и

проведем диаметры и поставим точки

и

и соединим их. Так как треугольник

равнобедренный, то

. Также

-внутренние накрестлежащие при параллельных прямых

и

и секущей

. Четырехугольники

-ромбы, так как треугольник

равен треугольнику

, так же эти треугольники равнобедренные. Из точек

проведем радиусы параллельно

поставим точки

.

.

- вертикальные. Хорды

и

параллельны, так как они стягивают равные дуги. Из точки

до пересечения с большой окружностью проведем биссектрису угла

. В месте пересечения поставим точку

. Угол

-центральный,угол

-вписанный, следовательно биссектриса

делит дугу

пополам.
Проведем общую биссектрису вертикальных углов

и

. Она будет начинаться в точке

, а заканчиваться предположительно в точке

.

параллельна

и параллельна

, так как

делит пополам дуги

и

.

, так как хорда

параллельна диаметру

и дуга

равна дуге

. Рассмотрим треугольники

и

. В этих треугольниках

– радиусы одной окружности,

, из доказанного известно, что

. Следовательно треугольник

равен треугольнику

. Если мы повернем треугольник

в точке

против часовой стрелки на

, то

совпадет с

,

совпадет с

, а

повернется на величину

, который в свою очередь равен

и прямая

станет прямой

.Значит биссектриса вертикальных углов

и

точно проходит через точку

.

- равные вписанные углы при равных центральных углах

и

. Из доказанного ранее известно, что

.Так как

- половина

, то

будет половиной

,а

– биссектриса

. Из этого следует, что

. Но хорда BS является биссектрисой не только

, но и

, значит

. Из доказанного ранее известно, что

, следовательно

.
Теперь из точки

проведем прямую параллельную

до пересечения с прямой

и поставим точку

, затем из точки

проведем прямую параллельную

до пересечения с прямой

и поставим точку
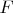
.

.
Наши углы

и

разделены на три равные части.
А на практике для деления

на три равные части достаточно найти точку

, построить треугольник

и провести прямые

и

.