Активное сопротивление проводника

[_PrizraK_]

Наткнулся на решение задачи по поиску активного сопротивления тонкостенного проводника (с учетом скин-эффекта), для двух случаев: сильного и слабого скин-эффекта.
Сначала пишутся ур-я Максвелла, которые приводятся к виду:
$\frac{\partial\mathbf{B}}{\partial t}=\frac{c^2}{4\pi\sigma\mu}\Delta\mathbf{B}$
$\frac{\partial\mathbf{E}}{\partial t}=\frac{c^2}{4\pi\sigma\mu}\Delta\mathbf{E}$
Затем пишут, что для периодического поля получаем уравнение Бесселя:
$\frac{\partial^2 E}{\partial r^2}+\frac{1}{r}\frac{\partial E}{\partial r} + k^2 E = 0$
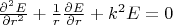
Откуда она получается, подскажите пожалуйста?

[warlock66613]

_PrizraK_, ну во-первых можно заметить, что от векторного уравнения перешли к скалярному. Этот переход вам понятен? (Можете проделать самостоятельно?)

[_PrizraK_]

Я понимаю, что расписали лапласиан:
$\Delta E = \frac{1}{r}\frac{\partial}{\partial r}(r \frac{\partial E}{\partial r}) = \frac{1}{r}\frac{\partial E}{\partial r} + \frac{\partial^2 E}{\partial r^2}$
Но откуда берется $k$? И почему дальше $k = \pm\frac{1-i}{\delta}$?

[warlock66613]

_PrizraK_, там написано, что поле предполагается именно периодическим? Потому что если поле не просто периодично, но изменяется во времени по гармоническому закону, то, учитывая линейность уравнений, это можно (удобно) записать так: $\mathbf E=(\operatorname{Re} E)\mathbf e_z$, где $E = E_0 e^{i \omega t}$. Тогда, если под $E$ понимать именно указанную комплексную величину (действительная часть которой и будет настоящим электрическим полем), всё срастается (проверьте).

[svv]

Тут, скорее всего, под $E$ понимается компонента $E_z$ вдоль проводника. Для неё как раз можно без проблем перейти от векторного волнового уравнения (или Гельмгольца) к скалярному, потому что единичный вектор вдоль проводника $\mathbf e_z$ константа.

[warlock66613]

А, ну да. Логично. Исправил выше.