Доброго всем времени суток. Уважаемые помогите с задачами:
1. На чашку пружинных весов осторожно кладут груз. Система начинает колебаться с амплитудой

. Каков период колебаний груза

?
Не совсем понятно, из намека в условии о том, что период зависит от амплитуды следует, что колебания не гармонические. Более ничего в голову не приходит.
2. На чашку, подвешенную к пружине с коэффициентом жесткости

, с высоты

падает груз массой

и прилипает к ней. Определить амплитуду

возникающих при этом колебаний чашки. Массой чашки пренебречь.
Нахожу скорость

, с которой груз упал на чашку и прилип к ней. С этой же скоростью чашка начала движение в момент
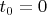
:
Из:

имеем:

, а т.к.

, то получим:

. Не сходится с ответом:

. Подскажите где я ошибаюсь?