Задача:Через блок, ось которого горизонтальна, перекинута верёвка длины

. За концы верёвки держатся две обезьяны, находящиеся на одинаковых расстояниях

от блока. Обезьяны начинают одновременно подниматься вверх, причём одна из них поднимается относительно верёвки со скоростью

, а другая со скоростью

. Через сколько времени каждая из обезьян достигнет блока? Массой блока и верёвки пренебречь; массы обезьян одинаковы.
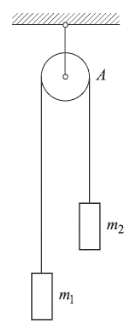 Мои рассуждения:
Мои рассуждения:Масса первой обезьяны:

, её начальная скорость относительно блока:

, её скорость относительно блока в момент движения:

, её скорость относительно верёвки в момент движения:

. Масса второй обезьяны:

, её начальная скорость относительно блока:

, её скорость относительно блока в момент движения:

, её скорость относительно верёвки в момент движения:

. Поскольку все силы уравновешиваются, то система двух обезьян изолирована. Тогда импульс системы до начала движения и после начала движения должен сохраняться. Тогда получаем:

, подставляем массы:

, массы сокращаются:

. Подставляем значения

и

, получаем:

, отсюда делаем вывод, что

. То есть, скорости движения обезьян относительно блока должны быть равны. Тогда

. Отсюда и выходит, что обезьяны одновременно достигнут блока. Время, затраченное на прохождение всего пути до блока:

. Верно ли такое рассуждение?