Имеем два подобных треугольника:

с углами:
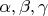
.
Условия данной темы не новы, но, побродив по интернету, я не нашел путного ответа как доказывается уравнение:

Уравнение для степени 2 справедливо только для прямоугольных треугольников, в силу справедливости Теоремы Пифагора

Если

Поставим задачу для степени 2 таким образом, что может это выведет на решение задачи для степени 3. Нужно доказать, что, при

, невозможно существование угла

со следующими свойствами:

Я полагаю, что задача может быть не сложная.