Введём 1-форму

Докажем, что форма

замкнута, по индукции. Будем использовать тождества:
![$\begin{array}{ll}\mathcal L_X \omega=\iota_X d\omega+d(\iota_X\omega)&(1)\\
\mathcal L_X\iota_Y\omega-\iota_Y\mathcal L_X\omega=\iota_{[X, Y]}\omega&(2)\end{array}$ $\begin{array}{ll}\mathcal L_X \omega=\iota_X d\omega+d(\iota_X\omega)&(1)\\
\mathcal L_X\iota_Y\omega-\iota_Y\mathcal L_X\omega=\iota_{[X, Y]}\omega&(2)\end{array}$](https://dxdy-03.korotkov.co.uk/f/e/f/f/eff933347e0792f786ba6707af70a91d82.png)

— тождество Картана,

— Frankel, The Geometry of Physics, Theorem 4.24.
Далее

— произвольные векторные поля из множества заданных

(чтобы не напрягать глаза, пытаясь разглядеть, какой там индекс у

).
База.

, так как

максимальной степени.

, учитывая

и

.
Шаг.
Пусть

(маленькое) — дифференциальная форма произвольной степени.
Из

с учётом
![$[X, Y]=0$ $[X, Y]=0$](https://dxdy-01.korotkov.co.uk/f/8/3/a/83ab41de21d9ee8b6370e81abb43ebf982.png)
:

Тогда, используя

:

Значит, если
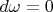
и

, то

.
Рассуждая по индукции, получим

. Следовательно,

В односвязной области отсюда получим

, где

— скалярная функция. Имеем

,
так как

обязательно совпадает с каким-то из полей

.
Итак,

является первым интегралом для любого

.
Ну, а дальше почти дословно переписывается
доказательство scwec, только

заменяем на

. Рассматриваем гиперповерхность

. Векторные поля

касательны к ней. Вводим на гиперповерхности набор 1-форм

, дуальных полям

, т.е. таких, что

. Имеем для любых

из нашего набора:
![$d\omega^i(X_k, X_\ell)=X_k(\omega^i(X_\ell))-X_\ell(\omega^i(X_k))-\omega^i([X_k, X_\ell])=0$ $d\omega^i(X_k, X_\ell)=X_k(\omega^i(X_\ell))-X_\ell(\omega^i(X_k))-\omega^i([X_k, X_\ell])=0$](https://dxdy-02.korotkov.co.uk/f/5/8/6/5861c2123310b9693adc66a334ef79c182.png)
Отсюда

, поскольку поля

в каждой точке гиперповерхности образуют базис. В односвязной области гиперповерхности

. Наконец,

при

Это означает, что у каждого векторного поля

есть ещё

первых интегралов

, где

(помимо найденного раньше

).