Не спорю, что лучший метод решения задач по геометрии - это опыт и внимательность.Однако, чтобы стать опытным, нужно не только решать много задач, знать теоремы, но и знать и уметь использовать очень полезные и мощные инструменты для решения планиметрических задач- методы.Лично я владею в совершенстве только одним простым методом - "через углы".Суть метода заключается в этом -берешь какой-нибудь известный угол, обозначаешь его, например

, и через этот угол выражаешь другие(типа угол

- некая система отсчета).Этот метод незаменим для геометрической оптики, где надо выразить неизвестный угол через известные.Или,например,им удобно "найти" внеписанную окружность.Пусть дан треугольник

и проведены прямые

и

, а внутри внешних углов, образуемыми этими прямыми и

две другие прямые пересекаются в точке

.Тогда чтобы доказать, что

- центр внеписанной окружности, достаточно доказать с помощью этого метода, что угол
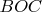
равен

(кстати, данная лемма доказывается также доказывается методом "через углы").К сожалению, данный метод далеко не универсален, и на олимпиадных задачах он встречается крайне редко.Вот мне и захотелось узнать некоторые методы от вас.Вот список, который я знаю:
1)Поворот
2)Параллельный перенос
3)Симметрии
4)Гомотетия
Опять же, владею я ими плохо, только "поворотом" немного попользовался - решил 2-3 задачи от силы.Я бы хотел попросить вас пополнить этот список, и,если надо, что-то в нем уточнить, и дать пару задачек, для "закрепления" этих методов.До этого попрошу привести примеры использования данных методов, особенно гомотетии(я слышал, что этот метод чрезвычайно полезен для решения задач с касающимися окружностями, а такие задачи весьма сложны даже для опытного геометра), т.к. не важно понять делали использования этих методов, сам я могу запросто что-то пропустить.