Базисы Грёбнера и решение систем полиномиальных уравнений

[maxal]

Ява-апплет, вычисляющий базисы Грёбнера, а также описание основ аппарата базисов Грёбнера и его применений, в частности, к решению систем алгебраических уравнений.

Алгоритмы для работы с базисами Грёбнера (как минимум алгоритм Бухбергера и его варианты) реализованы во многих математических пакетах, например, в коммерческих Magma, Maple и Mathematica и свободном Singular.

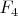
Материалы по алгоритмам Фужера (Faugère) $F_4$ и $F_5$:
описание: авторское описание алгоритма 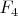$F_4$, алгоритма $F_5$, обзор Faugere's F5 Algorithm Revisited, а также теория и сравнение алгоритмов Бухбергера и Фужера (с упором на применение в криптографии);
реализация: есть в коммерческом пакете Magma, а также в авторской библиотеке FGb для Maple.

Альтернативные подходы к построению базисов Грёбнера и решению систем алгебраических уравнений:
Kronecker - библиотека для решения систем полиномиальных уравнений для пакета Magma.
Вычисление базисов Жанет и Грёбнера, а также решение систем полиномиальных уравнений (самостоятельные программы под Windows и Linux).
GINV (реализованный на C++ модуль языка Python) - инволютивное построение базисов Грёбнера идеалов и модулей в полиномиальных, дифференциальных и разностных кольцах. Имеется руководство пользователя на русском языке.

[maxal]

Здесь, конечно, имеет смысл упомянуть замечательный онлайновый солвер квадратных диофантовых уравнений от двух переменных (в частности, уравнения Пелля и их обобщения):
Quadratic two integer variable equation solver
Он умеет не только решать, но и расписывать решение по шагам.