Две соприкасающиеся тонкие симметричные стеклянные линзы -- двояковыпуклая и двояковогнутая -- образуют систему с оптической силой

. В отраженном свете длиной волны

наблюдают кольца Ньютона. Определить радиус m-го темного кольца.
Вот рисунок
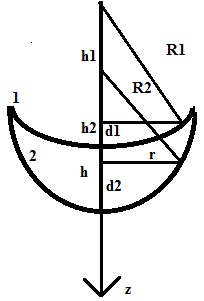
Пояснения к рисунку: 1. 1 и 2 --поверхности двояко-выпуклой и двояко-вогнутой линзы соответственно; 2.

и

-- катеты, соответствующие гипотенузам

и

, последние, кстати, являются радиусами кривизны линз и отсчитываются они от разных точек; 3.

-- искомый радиус кольца; 4.

и

равны

и

соответственно; 4. h -- промежуток между линзами.
Вопрос состоит в том, как найти

. Из рисунка очевидно, что

откуда

в предположении, что

и аналогично

,

. Теперь нужно найти разность хода. Я забыл её указать на рисунке, она выражается вот так:

. Вот теперь и встал вопрос о нахождении h. Наличие h связано с тем, что радиусы линз различны, поэтому пренебрегать им нельзя. Им пренебрегать нельзя ещё и потому, что

, т.е. с таким же успехом можно пренебречь и

. Короче говоря, я не знаю, как тут дальше.