Берём плоскость

с декартовыми координатами

, строим единичную окружность с центром в начале координат.
Точка

лежит на нашей окружности, если

.
Декартово произведение

— это множество упорядоченных пар точек

А декартово произведение нашей окружности на себя (даже не двух одинаковых!) — это множество таких упорядоченных пар точек

с координатами соответственно

, для которых


Итак, для ясности: и первая, и вторая точка в каждой паре принадлежит

. Сама пара принадлежит

.
Так как пара точек задаётся четырьмя числами, хочется рассматривать эту четвёрку как одну точку в

. Для этого мы естественным образом сопоставим каждой паре

из

одну точку

с декартовыми координатами

в

.
И — вот он, красавец-тор в

. Это двумерная поверхность, задаваемая в декартовых координатах

системой уравнений

Конечно, теперь можно переобозначить координаты в

как-то более привычно и получить, например:

Обратите внимание:

я ничего «существенного» не делал, только переобозначал;

то, что я делал, почти не выходит за рамки теории множеств, геометрии нет;

строить тор в

естественнее, чем в
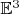
, здесь он в своём изначальном обличьи; полученный тор в

более симметричен, чем любой тор в
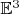
.