Уважаемые профессионалы и аматоры!
Инструментов для решения теоремы Ферма у современной математики нет, иначе она давно была бы решена. Конечно, ее доказал Уайлс с помощью эллиптических кривых и модулярных форм, но это до сих пор не раскрывает ее природы, а служит лишь фактом. Это многих не удовлетворяет и это замечательно, иначе бы человек перестал быть человеком.
Я приведу здесь доказательство для степени 3. Буду писать примитивно, уж простите.
Часть первая. Связанные множестваПусть множество

состоит из последовательности элементов

. Множество

состоит из последовательности элементов

. Попросту говоря, множество

есть последовательностью элементов

, а

вычетами этих соседних элементов. К примеру, для степени 3:


Применительно к связанным множествам

и

, запишем уравнение

в виде

где

и

есть элементами множества

а

– элемент множества

. Преимущества такого представления очевидны. Первое, мы охватываем все множество решений, так:

где

и

Второе, все значения

есть целочисленные, что безусловно очень ценно.
И наконец, из (1.5) вытекает условие решения ВТФ для степени 3, а именно если выполняется

для

, тогда есть решение (1.3), иначе – нет.
Очевидно, что условие решения (1.5) крайне обширно и охватывает как единичные элементы множества

так и их сумму. Таким образом из (1.6) получаем 2 явных условия:
Для
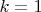
мы получим уравнение для соседних элементов

для
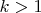
мы получим уравнение суммы элементов множества


Исследуем оба этих условия.
Часть вторая. Фигурные полиномыОднако современная математика далее бессильна, поэтому применим новые инструменты. Так, изучая множество

, находим что в результате вычета его соседних членов получается множество

, а вычеты его членов приводят к конечному результату 2. Для множества

мы получаем уже два множества вычетов –

и

, пока не придем к множеству конечного результата 6. Для степени 4 мы имеем уже три множества вычетов –

,

,

, пока не придем к множеству конечного результата 24. Для степени 5 мы имеем уже четыре множества вычетов –

,

,

,

, пока не придем к множеству конечного результата 120, и так далее.
Теперь действуем в обратном порядке, то есть выразим элементы множества

(это последовательность

) через константу 2, где получим формулу

А также найдем такую зависимость от константы 2 для элементов множества

(это последовательность

), где получим

Далее, выражая элементы множества

(это последовательность

) через константу 6 получим

И также найдем такую зависимость для элементов множества

(это последовательность

), где получим

Далее, выражая элементы множества

(это последовательность

) через константу 24 получим

И также найдем такую зависимость для элементов множества

(это последовательность

), где получим

Далее, выражая элементы множества

(это последовательность

) через константу 120 получим

И также найдем такую зависимость для элементов множества

(это последовательность

), где получим

И так далее.
Полученные зависимости позволяют нам вывести общие формулы для множеств

и

произвольной степени

, которые имеют разницу лишь в записи для четных и нечетных

. Таким образом, нами получен новый математический инструмент, который я назвал фигурными полиномами. Прежде чем обозначить его ценность для математики, разберемся в условных обозначениях:

- треугольное фигурное число или последовательность третьей диагонали треугольника Паскаля

- тетраэдральное фигурное число или последовательность четвертой диагонали треугольника Паскаля

- пентаэдральное фигурное число или последовательность пятой диагонали треугольника Паскаля

- гексаэдральное фигурное число или последовательность шестой диагонали треугольника Паскаля
Здесь верхний индекс, числа в круглых скобках, обозначают порядковый номер диагонали треугольника Паскаля, потому что

– диагональ единиц,

- ряд натуральных чисел.
Среди важных свойств фигурных полиномов следует отметить:
1. В состав фигурных полиномов входят фигурные числа, которые обладают очень важным свойством, а именно они являются числами-функциями, что значит, для каждого аргумента

есть свое значение

.
2. И самое главное, фигурные полиномы теперь стерли разницу между простым и составным числом, потому что теперь любое число множеств

, среди которых много простых чисел, может быть разложено в фигурный полином.
Продолжение следует. Комментируйте пожалуйста.