Здесь и далее

означает матричную алгебру над

размера

. Пусть у нас задано отображения типа

зафиксируем базис
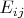
из матричных единиц в

тогда отображение полностью задаётся действием на следующих элементах

Если образно, то всё выглядит так: у нас есть две квадратные матрицы

размера

"разбитые" на блоки размера

(всего блоков, соответственно

). Чтобы "перемножить" две матрицы

"моим умножением" и получить новую матрицу

размера

нужно сделать следующее: взять в матрице

столбец

из

блоков размера

, в матрице

строку

из

блоков размера

, перемножить столбец на строку (!), получить матрицу размера

, и вставить полученный блок на "место"

в будущей матрице размера

, и так сделать со всеми строками и столбцами.
Интересуют любые свойства, аналогии, аллюзии и прочее подобного "умножения", рассматривалось ли где-нибудь что-то похожее? В частности, интересуют оценки на норму

через норму

(или норма отображения

в терминах первого абзаца).