Здравствуйте! Я уже несколько дней сижу над этими задачами, и все еще не получилось решить. Буду благодарна, если вы мне поможете.
1. На гладкой горизонтальной плоскости лежит доска
AB длины

, на конце
A которой находится небольшая шайба. Масса доски в

раз больше массы шайбы, коэффициент трения между ними

. Какую начальную скорость надо сообщить шайбе в направлении от
A к
B, чтобы она смогла соскользнуть с доски?
Здесь я с помощью закона сохранения импульса нашла, что

. Дальше, что ускорения равны

,

, где

- ускорение шайбы,

- ускорение доски.

. Если из последнего просто выражать

, то с ответом не сходится. Там нет лишней

.
2. На подставке лежит гиря массы
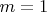
кг, подвешенная на недеформированной пружине жесткости

Н/м. Подставку начали опускать с ускорением

м/с

. Пренебрегая массой пружины, найти максимальное растяжение пружины в этом процессе.
В этой задачке я написала: по закону сохранения энергии:

, где

- максимальное растяжение пружины.

(1)=>

,

(2). Подставляя (2) в (1):

,

,

. Но в ответе совсем не так:

.
В идеале все решить через законы сохранения.