Riga писал(а):
Диэлектрики и проводники заполняют некий объём.
Задано распределение избыточных зарядов в диэлектриках. Дан избыточный заряд в металлах.
Вопрос - как находить граничное условие на металлах?


Здесь

- искомый потенциал (функция координат),

- диэлектрическая проницаемость (может быть как заданной константой, так и заданной функцией координат),

- поверхность

-го проводника,

,
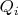
- заданные потенциал и заряд

-го проводника,

- внешняя нормаль.
Цитата:
Интересует численный подход. Т.е. будет как-то считаться поле в диэлектриках, но для этого нужно знать граничное условие на металлах, будь то в потенциальной постановке, будь то в векторной.
Маленький вопрос - справляться с бесконечностью в вакууме вне этого объёма с металлами и диэлектриками можно только задав большую область и сделав граничные условия нулём?
Задав большую область и положив потенциал на ее границе равным нулю, Вы получите постановку задачи для такой физической ситуации, когда вышеупомянутые проводники и диэлектрики, заключаются в заземленную проводящую оболочку, внутренняя граница которой является (внешней) границей этой большой области. Решение для такой физической ситуации будет, естественно, отличаться от решения для исходной ситуации (т.е. без проводящей оболочки). Чам больше область, тем меньше отличие.
Однако можно вместо этого задать область в виде (например) шара и задать на его границе распределение потенциала, равное сумме потенциалов от располженных в центре шара точечного заряда, равного суммарному заряду диэлектриков и проводников, и точечных мультипольных моментов до порядка

, равных соответствующим мультипольным моментам распределения заряда в диэлектриках и на проводниках. При этом чем больше

, тем больше точность (для фиксированного радиуса шара). И, например, при

(только точечный заряд) для достижения такой же точности, что и при задании нулевого потенциала, потребуется (думаю, что гораздо) меньшая область.