Полученное утверждение:
Цитата:
(70) числа

и

являются квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

можно упростить и свести к утверждению:
Цитата:
(70.1) числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Это достигается в следующем сообщении из упомянутой темы (которое мы модифицировали для нашего случая):
Мы получили (70) из того, что среди чисел

некоторое число, сравнимое с

следует за числом, сравнимым с

, и некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Но также верно, что среди чисел

либо некоторое число, сравнимое с

следует за числом, сравнимым с

, либо некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Рассматривая второй сомножитель в равенстве (28), умноженный на

, получим, что либо

либо

сравнимо с квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю идеала

.
Cравнивая это утверждение с (70) получим, что числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю идеала

.
Поскольку

- произвольный простой идеал, делящий

, то числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю

.
Перемножая сравнения

, для

, где

- целое алгебраическое число поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, получим, что числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Последнее утверждение эквивалентно (70.1).
Что и требовалось.
Следующее сообщение из упомянутой темы рассматривает простое число

, которое делит

(а не

), и на которое делятся не все коэффициенты

:
Пусть

, где

или
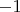
.
Пусть

- нечётный простой делитель числа

, на который делятся не все коэффициенты

.
Пусть

разлагается в произведение главных идеалов поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
.
Наша цель получить результат, аналогичный (70), который мы получили в предыдущем сообщении.
Пусть

,

, где целое число

сравнимо с

по модулю

.
Тогда

.
Из равенства
(3)
![$x^2-\sqrt[n]{4} y z=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$ $x^2-\sqrt[n]{4} y z=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$](https://dxdy-03.korotkov.co.uk/f/6/7/6/676a5fb8958ff4284fc13d636fc7331e82.png)
следует сравнение
(3.1)

,
поскольку

.
Из (3.1) следует:
(3.2)

, где целое число

сравнимо с

по модулю

.
В самом деле

.
Пусть

- какой-либо простой идеал поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, делящий

.
Из сравнений (III) в теме "Поиск доказательства ВТФ для

обзорная тема 1", которые выполняются в силу леммы 2 в названной теме, и того, что не все коэффициенты

делятся на

следует, что не все числа

в равенствах (II) равны нулю.
Значит не все числа

сравнимы между собой по модулю идеала

.
Следовательно, часть из них сравнима с

, а другая часть сравнима с

по модулю идеала

.
Расположим числа

по кругу, так чтобы первое число следовало за последним.
Тогда обязательно некоторое число, сравнимое с

следует за числом, сравнимым с

, и некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Значит среди чисел

некоторое число, сравнимое с

следует за числом, сравнимым с

, и некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Числа

и

делятся на

.
Эти числа, соответствующие второму сомножителю в равенстве (28) нас не интересуют.
Нас интересуют числа

и

, соответствующие первому сомножителю в равенстве (28), умноженному на

.
Эти числа, сравнимые соответственно с

и

по модулю идеала

, являются квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, в силу (62).
Поскольку

и

, то числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю идеала

.
Поскольку

- произвольный простой идеал, делящий

, то числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю

.
Перемножая сравнения

, для

, где

- целое алгебраическое число поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, получим:
(70.x) числа

и

являются квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Как и утверждение (70), утверждение (70.x) можно свести к утверждению:
Цитата:
(70.1) числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Завершает доказательство нашего улучшенного результата следующее сообщение из упомянутой темы:
Пусть

, где

или
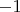
.
Пусть

- простое число, по модулю которого числа

и

не сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
.
Покажем, что

не может делиться на

.
Предположим обратное, что

делится на

.
Если не все коэффициенты

делятся на

, то выполняется утверждение (70.x), которое противоречит условию, что

не сравнимо с квадратом целого алгебраического числа поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
В самом деле, из утверждения (70.x) следует, что числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Деля второе число на первое, получим: число

сравнимо с квадратом целого алгебраического числа поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

, что противоречит условию.
Значит все коэффициенты

делятся на

.
Тогда

.
Из утверждения (62.b):
(62 b) число

является квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю любого нечётного простого числа

, которое разлагается в произведение главных идеалов этого поля.
следует, что число

сравнимо с квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю

.
Перемножая сравнения

, для

, где

- целое алгебраическое число поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, получим:
Число

сравнимо с квадратом целого алгебраического числа поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Что противоречит условию.
Что и требовалось.
Теперь мы можем усилить теорему 6 из темы "Поиск доказательства ВТФ для

обзорная тема 1",
заменив условие:
Цитата:
Пусть

делится на простое число

, по модулю которого
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует, и среди вычетов

есть квадратичные и неквадратичные.
на условие
Цитата:
Пусть

делится на простое число

, по модулю которого среди вычетов

есть квадратичные и неквадратичные.
То есть уже не требуется несуществования
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
по модулю

.
Но следует добавить к условиям теоремы 6 то, что

делится на

, и что число

разлагается в поле
![$\mathbb{Q}[\sqrt[n]{2}, i_n]$ $\mathbb{Q}[\sqrt[n]{2}, i_n]$](https://dxdy-04.korotkov.co.uk/f/7/1/9/719b7ec7c5cd22a322630ab38e60d4a882.png)
на простые идеалы, которые являются главными.