Пример:

,

. Таблица
![$g = [ [1, 2], [3, 2], [1, 3], [1, 2] ]$ $g = [ [1, 2], [3, 2], [1, 3], [1, 2] ]$](https://dxdy-01.korotkov.co.uk/f/4/c/1/4c19035e3ef40ec2ed5443473dfa85b382.png)
, где
![$g[0][1] = 2$ $g[0][1] = 2$](https://dxdy-01.korotkov.co.uk/f/4/7/8/478a234537a3ffeaa7fa7e0e90d711fd82.png)
, означает что у вершин

и

есть ветка с номером

. Ответ будет да(true), т.к. сущ. нт

, можно взять путь(набор ребер)

, тогда если применить этот путь к любой вершине включая саму нт, то мы попадем всегда в нее.
Я ее решил простым перебором, но хотелось бы узнать есть ли лучший метод ?
Условие на самом деле можно понять. Есть матрица

размера

. Путь - это последовательность чисел от

до
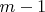
. Чтобы пройти по пути

, начиная из вершины

, нужно сначала пойти по ребру номер

из вершины

, то есть оказаться в
![$v = A[u][p_1]$ $v = A[u][p_1]$](https://dxdy-01.korotkov.co.uk/f/4/8/c/48cf631d750fa081fd2bdb7f6903614182.png)
. Далее нужно сделать шаг по ребру номер

из новой вершины, то есть оказаться в
![$w = A[v][p_2] = A[A[u][p_1]][p_2]$ $w = A[v][p_2] = A[A[u][p_1]][p_2]$](https://dxdy-02.korotkov.co.uk/f/d/a/a/daa7264880e30fc56bc1333e57e11b0982.png)
. И так далее. Назовём

конечную вершину пути

, который мы начали в вершие

.
Вопрос в том, есть ли такая последовательность

, что

.
Это комментарий для тех, кому сложно понять условие (я тоже не с первого раза понял, но разобрался). Как решать - не знаю.