треугольник

[kel]

ничего простого в голову не приходит
Дан треугольник АВС, О - точка пересечения бисектрис. Угол АОС равен 135 градусов. Найти Угол АВС треугольника.

[AD]

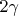
Обозначьте три угла треугольника $\triangle ABC$ через $2\alpha$, $2\beta$ и $2\gamma$, расставьте их на рисунке треугольника с проведенными биссектриссами, и, примените два раза теорему о сумме углов треугольника. Уравнений будет два на три неизвестных, но нужный угол найти из нее можно.

Добавлено спустя 1 минуту 25 секунд:

При желании можете в общем виде решить, для произвольного угла $\angle AOC$.

[kel]

[Nephi]

Сделайте обозначения, как рекомендовал AD. Сумма углов в треугольнике равна 180 градусам. Примените эту теорему для треугольников АВС и АОС.