Ошибка интерполирования функции

полиномом

в точках

(

) на отрезке
![$\left[ a,b \right]$ $\left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/9/f/b/9fb84e4297cfbcdc1186ca6b114843db82.png)
равна
![$$\[f\left( x \right)-p\left( x \right)=\frac{{{f}^{\left( n+1 \right)}\left( \xi \right)}}{{\left( n+1 \right)!}}\prod\limits_{k=0}^{n}{\left( x-{{x}_{k}} \right)}\]$$ $$\[f\left( x \right)-p\left( x \right)=\frac{{{f}^{\left( n+1 \right)}\left( \xi \right)}}{{\left( n+1 \right)!}}\prod\limits_{k=0}^{n}{\left( x-{{x}_{k}} \right)}\]$$](https://dxdy-01.korotkov.co.uk/f/0/b/0/0b031797ce8eb2a385b73ba5acaf0d1482.png)
где
![$\xi \in \left[ a,b \right]$ $\xi \in \left[ a,b \right]$](https://dxdy-02.korotkov.co.uk/f/d/a/5/da5a1df655a463c475e9d6909213dd2e82.png)
. Правда, это верно, только если

— функция из
![${{C}^{n+1}}\left[ a,b \right]$ ${{C}^{n+1}}\left[ a,b \right]$](https://dxdy-03.korotkov.co.uk/f/2/a/5/2a50041c4be8b60d25e5b3e651364f5182.png)
.
Выбор Чебышевских узлов продиктован желанием минимизировать значение произведения
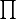
в правой части равенства. Это не означает, что такой выбор оптимален в каждом конкретном случае, наоборот, для конкретной функции гораздо оптимальнее найти свои точки аппроксимации. Всё дело во множителе перед произведением
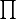
: положение точки

так же зависит от всех узлов аппроксимации. Кроме того, чем хуже ведёт себя производная

, тем хуже будет аппроксимация.
А производные функций имеют свойство с ростом порядка себя вести всё хуже и хуже. Кажется, вот мы взяли многочлен большей степени, а аппроксимировать он стал только хуже. Из сказанного это не удивительно. Поэтому люди придумали замечательный метод: сплайновая интерполяция. Вместо того, чтобы брать один полином большой степени, возьмём много полиномов маленькой степени, каждый на своём участке значений аргумента функции. На стыках краёв полиномов потребуем их гладкого сочленения, гладкость выбирается исходя из назначения аппроксимации (до 1-ой производной, до 2-ой и так далее). Такой подход в подавляющем большинстве случаев оказывается одновременно и проще, и продуктивней.
В вашем же случае функция — корень из модуля — вообще не является дифференцируемой функцией и не подпадает под формулировки теоремы. Но если вы её немного подправите:

где

— малая величина, то обнаружите, что производные ведут себя в нуле очень плохо. Выбор Чебышевских узлов интерполяции не даст ничего, так как максимальное значение производной стремиться к бесконечности. Так что использование сплайнов здесь просто напрашивается само собой.