Здравствуйте, подскажите, правильно ли я нашел параметр

?
Случайная величина

имеет плотность распределения вероятностей:

Определить параметр a. Найти функцию распределения. Вычислить
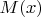
и

.


Я сомневаюсь в том, правильные ли пределы я интегрирования я взял?