А откуда Вы берете

? Типа одно подстрока другого?
Ну, я это заключаю из того, что... да, что одно подстрока другого)
Ну да... может оно тут лишнее даже, но по способу заключения это разве не такое же утверждение, как

? Мы же понимаем это непосредственно видя, что

содержит элемент

?
-- 11.11.2015, 18:02 --По поводу исходной задачи:

Рассмотрим левую часть.
Пусть

.
Тогда, либо

, либо

.
1). Если

, то

и
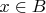
.
Тогда

и

(по определению объединению).
Следовательно

.
2). Если

, то так же

и

.
Получаем, что во всех случаях, когда

, также

.
То есть

.
Обратно.
Пусть

, тогда

и

.
Если

, то

или

.
Если

, то
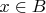
или

.
Возможны следующие случаи:
1).

,
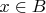
.
Тогда

.
2).

,

.
Тогда

.
3).

Тогда

.
4).

,
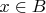
Тогда

.
(В принципе достаточно рассмотреть только два варианта 1) и 3))
Так как во всех случаях, когда

, также

.
Это значит, что

.
Из

и

Следует, что

Такое доказательство подразумевалось под подробным?