Каждое неприводимое представление группы

характеризуется парой целых чисел

Оно изображается графически на плоскости

в виде фигуры, ограниченной шестиугольником: три стороны имеют длину

единиц, а другие три — длину

единиц (рис. 4.4,
а). Шестиугольник вырождается в равносторонний треугольник, если

или

равно нулю (рис. 4.4,
б,
в). Граница фигуры симметрична относительно отражения в оси

Напомним, что неприводимое представление группы

характеризуется одним целым числом

; графически оно изображается прямым отрезком длиной

единиц. На нем расположено

точек, каждая из которых соответствует одному состоянию. Для представления

группы

кратность состояния, отвечающего точке на плоскости

определяется следующим правилом: точке, лежащей на границе, соответствует одно состояние; точке, принадлежащей второму (если считать от границы внутрь) слою, — два состояния; третьему слою, — три и т. д. до тех пор, пока не будет достигнут треугольник. После этого кратность перестает увеличиваться и остается равной

при

(или

при
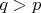
).