Мда... Ясно пока лишь то, что каша у меня в голове одна, да притом приличная. Сейчас попробую разобраться.
Рассмотрим интервал

.
Не рассмотрим. Не удастся, т.к. число — ни разу не интервал.
А можем тогда рассмотреть интервал, допустим,

с границами

и

(

) и сказать, что если для интервала

найдётся некоторое число, скажем,

внутри этого интервала, то для любого

точка

(это, кажется, следует из аксиом, описывающих операцию сложения и отношение порядка — пока не было времени глубже в этом разобраться)?
А дальше представляем, что

, и тогда нам снова есть о чём говорить, как мне кажется.
Зорич в данном случае — не лучший вариант.
Однако исходить приходится из того, что как раз по Зоричу мы и идём (вернее, по конспекту, сделанному на его основе, иначе я бы раньше выполнил совет
Hasek).
Мы формулировали аксиому Архимеда так: "Множество натуральных чисел неограниченно".
Это бессмысленная формулировка. В том смысле, что оно не ограничено по самому своему определению. Выберите любую из вменяемых формулировок той аксиомы.
А вот тут сложно. И мой лектор, и Зорич формулируют эту аксиому как теорему и выводят из другой теоремы, теоремы о существовании точной верхней грани (лектор даёт ей название "принцип полноты Вейерштрасса"), которая, в свою очередь, выводится из аксиомы полноты, как вы и сказали, в варианте Дедекинда, разве что только в такой формулировке, что теория сечений не затрагивается. А дальше есть существенное различие: во-первых, Зорич выводит неограниченность натуральных чисел сверху, неограниченность целых чисел сверху и снизу, а потом формулирует принцип Архимеда так: "Если фиксировать произвольное положительное число

, то для любого действительного числа

найдётся и притом единственное целое число

такое, что

Подход лектора отличается, он говорит, что сам принцип Архимеда заключается в том, что

не ограничено сверху, а, как следствие,

существует

И единственное, что мне пока непонятно, это почему вы считаете вторую формулировку бессмысленной. Я пытался думать в эту сторону, и, честно, не смог представить конечного индуктивного множества, и интуитивно я согласен, что смысла в этом особо нет. Впрочем, я уже вооружен знанием, что интуиция частно плохо срабатывает. Наверно, надо смотреть в сторону множеств, на которых не выполняются аксиома полноты и/или они неупорядочены, но для меня это пока слишком сложная материя. Возможно, всё станет яснее, когда я попытаюсь выводить нашу аксиому полноты как теорему, приняв, как сказал лектор, одновременно и принцип Архимеда, и принцип полноты Вейерштрасса за аксиому, но пока это тоже в сторону.
если аксиома Архимеда не выполняется
Не очень понятно, как именно вы хотите прийти к требуемому выводу. Несколько напоминает доказательство от противного, но там-то схема другая — если из отрицания
вывода следует отрицание посылки, то из посылки следует вывод, если я сколь-нибудь понятно изъясняюсь. Отрицать же посылку, как это делаете вы, бессмысленно — даже если вы выведете из этого отрицания чего интересного, решению задачи это ничем не поможет.
Наверно, я снова невнятно выразился... Вот увидел я аксиому в нашей формулировке: "Множество

не ограничено сверху". И в задании сказано: "Доказать, используя аксиому Архимеда". Наверно, я должен предположить что-то, исходя из чего аксиома будет нарушена. Из чего она может быть нарушена? У нас есть следствие:


Значит, если

не может превысить некоторого значения, то и

не потребуется сколь угодно большим. Так я только пришёл к тому, откуда брать ограничение на

.
Теперь ещё раз смотрю на задание: во всяком непустом интервале содержится рациональное число. Для начала я просто решил доказать, что в любом непустом интервале может быть какое-то число. А для этого уже взял интервал

и стал показывать, что существуют такие
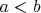
, что

(если бы таких

не существовало, то нарушалась бы неограниченность

сверху, что я и пытался показать в первой части первого сообщения). Так что, мне кажется, что отрицал я вывод и получил отрицание посылки (кстати, спасибо в этом месте: я раньше меньше задумывался над сутью метода "от противного").
у меня есть процедура нахождения рационального числа между двумя другими рациональными
Само по себе это ещё не доказывает исходного утверждения. А что доказывает? Ну, например, если между двумя рациональными числами вы б научились вставлять много-много, и притом часто-часто...
Допустим, я умею вставлять их часто-часто. А как показать, что кого-то нельзя будет вставить настолько чаще, что между этими двумя "кем-то" не останется зазора для рационального числа? У меня получается только, что повторённое несколько раз постепенно становится истинным: для всякого

можно найти меньшее число, так почему бы этому меньшему числу не быть рациональным... Наверно, отмету эту процедуру за ненадобностью, надо просто будет модифицировать первую часть так, чтобы найденное число имело вид

.