I don't understand this: " When grey disk is still, the A point is always up at the end?"
It concerns to balancing, the position of A when all disks are still.
The point A can't be at top always because the purple disk don't turn in the laboratory reference.
Well. Am I right:
1. Initially the both disks are still.
2. Then you give gray some angular acceleration till it angular speed reaches w0 and look to purple.
One can project the vector of gray disk angular speed
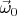
(as angular acceleration too) to purple disk coordinate system. The
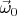
component along the purple axis is
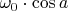
.
The component perpendicular to the axis is
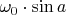
. This one gives us nothing.
But, if friction if purple disk axle would be zero, the frist component gives pruple disk the rotation
relative to gray disk with angular velocity
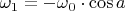
. Due to friction momentum, this rotation will cease down to zero. If fruction is quite big, the total relative rotation angle will be quite small. Exact value depends on values of friction momentum,

,

and spinup angular acceleration

and some other subtle things.