Предел отношения k(p)/p k ~ корень (k+c)^p=qk^p

[2old]

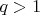
Пусть $c>0$ и $q>1$ - фиксированные числа, Для каждого натурального $p$ обозначим через $k(p)$ наименьшее среди таких натуральных $k$, для которых выполняется неравенство $(k+c)^p\leq qk^p$. Доказать, что существует предел $\lim\limits_{p\to\infty}\frac{k(p)}{p}$ и найти его.

1. Для начала я решил найти такое $k$ хотя бы для первых двух степеней и посмотреть на него. Получилось для
$p=1\rightarrow k(1)=\lceil\frac{c}{q-1}\rceil$
$p=2\rightarrow k(2)=\lceil\frac{c}{q-1}(1+\sqrt{q})\rceil=\lceil\frac{c}{\sqrt{q}-1}\rceil$

2. Для $k=k(p)$ можно записать такое неравенство $k^p\leq(k+c)^p\leq qk^p$. Но что с ним делать я не придумал, хотя хочется как-то присобачить теорему о двух милиционерах.

3. Из геометрических соображений "ясно", что положительный корень у $(k+c)^p=qk^p$ будет один. Отсюда $k=\lceil\frac{c}{q^{1/p}-1}\rceil$
Можно посчитать предел $\lim\limits_{p\to\infty}\frac{c}{q^{1/p}-1}\cdot\frac{1}{p}$. У меня получилось $1$

Вот в общем-то все мысли :(

[ИСН]

Пункт 3, в общем, исчерпывающе раскрывает тему (предыдущие пункты не нужны). Осталось правильно найти предел. Вам не кажется странным, что он получился не зависящим ни от $q$, ни от $c$?

[2old]

ИСН
Да, я за знак предела выносил и забыл. Получается так:

$$\lim\limits_{p\to\infty}\frac{c}{q^{1/p}-1}\cdot\frac{1}{p}=\lim\frac{c}{e^{1/p\ln{q}}-1}\cdot\frac{1}{p}=\lim\frac{c}{1/p\ln{q}}\cdot\frac{1}{p}=\frac{c}{\ln{q}}$$

А как строго показать, что там будет один корень?

[Cash]

При извлечении корня (возведения в степень) вы положительных корней точно не потеряете.

[2old]

Cash
Да, спасибо. Просто я численно погонял и там отрицательный корень активно к $0$ подбирается, засомневался немного поэтому.