yurka писал(а):
множество
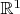
неизмеримо и его мера - континиум вроде
Как мера может быть "контин
уум", когда она есть число?? Вы не путаете меру и мощность?
yurka писал(а):
рациональные числа измеримы, так как их можно представить в виде измеримого подмножества целых чисел, то есть m/n, а что дальше?
С каких это пор рациональные числа стали подмножеством целых? Я вроде не очень давно первый курс заканчивал, но у нас было наоборот.

yurka писал(а):
как мерять измеримое множество?
Как доказывали измеримость - так и меряйте. Если вы доказали, что внешняя мера равна внутренней - так вот их общее значение и равно мере. Если вы доказали, что множество получается известными теоретико-множественными операциями из уже измеренных множеств, и, таким образом, измеримо - ну так смело используйте согласованность меры с этими операциями (аксиомы аддитивности меры, теоремы о непрерывности меры, итп). Если доказали, что ваше множество - подмножество множества нулевой меры, то оно и само будет измеримо и иметь нулевую меру. Еще вопросы?