Все. Решил. Вроде бы. С полными выкладками своих рассуждений. Проверьте кому не лень именно ход.
Арифметика- не страшно, ее можно всегда быстро поправить.

Рассмотрим поведение функции. в данном интервале.
(кольцо представленное окружностью до первой критической точки)

От точки разложения

ближайшей точкой(из особых) является точка

На основе данного факта и сформирована данная окружность.
Функция

разложена на две простые дроби.

Обе данные функции не встречаются с особыми точками на интервале

т.е для обоих выполняется условие

Где

соответствующая особая точка для каждой из двух функций.
(Т.е радиус изменения

(от точки

) меньше радиуса от точки

до ближайшей особой).
Разложение ведется по формуле:
Если

т.е как бы изменение z не превосходит



Сопоставим с формулой: В нашем случае


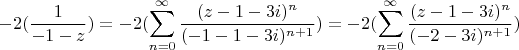

В нашем случае



Итого в круге


От особой точки z=0 до точки z=-1 образуется интервал, представленный кольцом. Рассмотрим как ведут себя функции

и

внутри кольца
Точка z=0 является особой для второй функции. Точка 0 не является особой для первой функции. По этому разложение

внутри кольца остается таким же, как и разложение внутри круга.
Остается разложить

в данном интервале. Данная функция как бы уже вывалилась за особую точку.
Т.е выполняется равенство

в нашем случае

В такой ситуации разложение ведется по формуле.

Разложим

В нашем случае

и

Тогда

Итого в кольце


Окружающая бесконечность. Сдесь уже для обоих функций выполняется условие

Т.е обе функции как бы вывалились за свои соответственные особые точки.

Условие

уже выполнялось для \frac {-1} {z} внутри кольца. Сдесь оно тоже выполняется, по этому разложение будет таким же как и в кольце.
Разложим

Итого
