Контрольные вопросы

[AD]

[Прежде всего, обращаюсь к товарищам модераторам, потому что не знаю, куда бы положить эту тему. Для "олимпиадных" вроде бы простая слишком ... а, может быть, вообще куда-нибудь в "свободный полёт" лучше ...]

Хочется поделиться всякими хитрыми (и глубоко праздными) вопросами, которые мне приходили в голову в-основном в процессе подготовки к экзаменам, хотя не только. Вопросы простые, но при первом прослушивании действуют неплохо. Особенно когда сидит кто-нибудь перед экзаменом, думает, что всё выучил, а тут такой вопрос подкинуть - и сразу... Ну, короче, можно отличить "зубрильщиков" от "истинных" "мегаботанов".

Ясно, что на старшее поколение большинство этих вопросов впечатления особого не произведут, потому что они уже в этом настолько давно разобрались, и это кажется банальностью. Вопросы в-основном некорректные, намеренно запутывающие.

1. Верно ли, что прямое произведение $\mu\otimes\nu$ полных мер $\mu$ и $\nu$ - полная мера?
Подтекст: Этот вопрос возник перед экзаменом по теории меры и интеграла. Многие готовились по книжке Дьяченко и Ульянова, там в при доказательстве теоремы Фубини в условии была дана полнота исходных мер, а про полноту их произведения ничего не говорилось, но она использовалась. Осознание правильного ответа всегда приводило в легкое удивление

2. Пополненная числовая прямая $\mathbb{R}\sqcup\{+\infty,-\infty\}$является компактным множеством (из любого открытого покрытия можно выбрать конечное подпокрытие), но не является ограниченным множеством (не содержится ни в каком шаре). ?!
Подтекст: Этот вопрос интересен, когда уже изучены метрические пространства, и в голове крепко сидит штамп, что всякий компакт - замкнутое ограниченное множество, но топологические пространства еще на вялом уровне. Многие приходят в ступор, хотя для ответа достаточно пройтись по доказательству ограниченности компакта.

3. Пусть дано выборочное пространство $\Bigl(X,\mathcal{F},\{P_\theta\}_{\theta\in\Theta}\Bigr)$. Выборка $X_1,\ldots,X_n$ обычно предполагается набором независимых одинаково распределенных случайных величин на этом пространстве. При каком/каких $\theta$ они должны быть независимыми? При всех $\theta\in\Theta$? При каком-то одном? При "истинном"? Ведь случайные величины могут быть независимыми по одной мере, а по другой зависимыми?
Подтекст: Большинство, конечно, слышало правильный ответ на этот вопрос, но далеко не все его смогли воспроизвести перед экзаменом по статистике. Удаётся запутать, навязав в формулировке неправильную картинку.

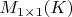4. Будет ли кольцо матриц $M_{n\times n}(K)$ над неассоциативным кольцом $K$ само ассоциативным? Могу доказать: ведь каждой матрице $A\in M_{n\times n}(K)$ соответствует отображение $\mathcal{A}:K^n\to K^n$, $x\mapsto Ax$, а произведение отображений ассоциативно, а произведение матриц как раз списано с произведения отображений. С другой стороны, ясно, что даже кольцо $M_{1\times1}(K)$ неассоциативно.
Подтекст: Этот вопрос пришел в голову при просмотре вот этой темы на нашем форуме, и пока я его не очень еще успел опробовать. Такое доказательство ассоциативности произведения матриц нередко приводят первокурсникам (в качестве альтернативы прямому вычислению), но вот, оказывается, в нем есть такой подводный камень.

_________

Если еще вспомню - буду дописывать.

[Профессор Снэйп]

AD писал(а):

2. Пополненная числовая прямая $\mathbb{R}\sqcup\{+\infty,-\infty\}$является компактным множеством (из любого открытого покрытия можно выбрать конечное подпокрытие), но не является ограниченным множеством (не содержится ни в каком шаре). ?!
Подтекст: Этот вопрос интересен, когда уже изучены метрические пространства, и в голове крепко сидит штамп, что всякий компакт - замкнутое ограниченное множество, но топологические пространства еще на вялом уровне. Многие приходят в ступор, хотя для ответа достаточно пройтись по доказательству ограниченности компакта.

Пополненная числовая прямая гомеоморфна отрезку $[0,1]$. Какие там ещё "подтексты", зачем людей пугать?

AD писал(а):

4. Будет ли кольцо матриц $M_{n\times n}(K)$ над неассоциативным кольцом $K$ само ассоциативным? Могу доказать: ведь каждой матрице $A\in M_{n\times n}(K)$ соответствует отображение $\mathcal{A}:K^n\to K^n$, $x\mapsto Ax$, а произведение отображений ассоциативно, а произведение матриц как раз списано с произведения отображений. С другой стороны, ясно, что даже кольцо $M_{1\times1}(K)$ неассоциативно.
Подтекст: Этот вопрос пришел в голову при просмотре вот этой темы на нашем форуме, и пока я его не очень еще успел опробовать. Такое доказательство ассоциативности произведения матриц нередко приводят первокурсникам (в качестве альтернативы прямому вычислению), но вот, оказывается, в нем есть такой подводный камень.

В неассоциативном случае произведение матриц соответствует отображению, которое может не совпадать с композицией отображений, соответствующих каждой из перемножаемых матриц.

Неинтересные вопросы.

[AD]

Профессор Снэйп писал(а):

Неинтересные вопросы.

Warned. Предупреждал типа.

AD писал(а):

Ясно, что на старшее поколение большинство этих вопросов впечатления особого не произведут, потому что они уже в этом настолько давно разобрались, и это кажется банальностью. Вопросы в-основном некорректные, намеренно запутывающие.

Контрольные вопросы - это всегда вопросы "к какому-нибудь курсу". Или "по пройденной теме".

Профессор Снэйп писал(а):

Пополненная числовая прямая гомеоморфна отрезку $[0,1]$.

Вот это был вопрос по теме "метрические пространства". Причем тут вообще этот факт, кстати? Нужно дать точный ответ!

Добавлено спустя 2 минуты:

Вопросы не для решения, а для подкалывания сокурсников. И для формирования более глубокого понимания курса. Сочинение таких вопросов гораздо полезнее узнавания ответа.

[Brukvalub]

Есть целые книжки "неожиданных вопросов". Например, Гелбаум Б., Олмстед Дж. — Контрпримеры в анализе Секей Г. — Парадоксы в теории вероятностей и математической статистике, было бы утро - вспомнил бы еще....

[tolstopuz]

Brukvalub писал(а):

было бы утро - вспомнил бы еще....

http://lib.mexmat.ru/books/390

[AD]

Классический контрольный вопрос описан еще в известном анекдоте:

Цитата:

Одного понять не могу - как керосин по проводам течёт?

Да, книжки - в тему. Особенно

Brukvalub писал(а):

Парадоксы в теории вероятностей и математической статистике

Добавлено спустя 2 минуты 35 секунд:

Кстати, может, первый вопрос, после озвучивания правильного его решения здесь, пообсуждать по-подробнее ..? Дело в том, что в разных науках на него дают, видимо, разные ответы. Произведение мер по-разному определяется. Можно обсудить плюсы и минусы.

[lofar]

Меры.
Пусть мера $\mu$ определена на $\sigma$-алгебре $\mathfrak M$, а мера $\nu$ определена на $\sigma$-алгебре $\mathfrak N$. $\mathfrak M\times\mathfrak N$ определяется как $\sigma$-алгебра порожденная множествами вида $A\times B$, $A\in\mathfrak M$, $B\in\mathfrak N$. Если $\mu$ и $\nu$ $\sigma$-конечны, то существует единственная мера $\lambda$ на $\mathfrak M\times\mathfrak N$, такая, что $\lambda(A\times B)=\mu(A)\nu(B)$, для любых $A\in\mathfrak M$ и $B\in\mathfrak N$.

Обычно, по определению полагают $\mu\times\nu=\lambda$. При таком определении произведение мер не обязано быть полным. Классический пример. Возьмем неизмеримое по Лебегу подмножество прямой $C\subset\mathbb R$, тогда $C\times \{0\}$ будет неизмеримо в произведении $\mathbb R\times\mathbb R$, в месте с тем $C\times \{0\}$ содержится в измеримом множестве $\mathbb R\times \{0\}$, имеющем меру $0$.

С другой стороны, всякую меру можно каноническим образом пополнить. Если хочется иметь дело только с полными мерами, то можно сразу определить $\mu\times\nu$ как пополнение $\lambda$.


Матрицы.
На мой вкус, интереснее отметить другой факт (для многих, как показывает практика, удивительный). Пусть $R$ ассоциативное кольцо и $R^n$ --- множество векторов-столбцов длины $n$. Для всякой матрицы $A\in M_n(R)$ определена функция $f_A\colon R^n\to R^n$, $f_A(x)\mapsto Ax$. Так вот, если $R$ не коммутативно, то $f_A$ не обязана быть линейной (предполагается, что скаляры множатся на векторы слева, т. е. $R^n$ рассматривается как левый $R$-модуль). Линейной будет функция $g_A\colon x\mapsto(x^tA)^t$ ($t$ --- транспозиция). Как и в коммутативном случае отображение $g\colon M_n(A)\to End(_RR^n)$, $A\mapsto g_A$ является биекцией между кольцом матриц и кольцом линейных операторов на $_RR^n$. Важно, что это отображение не изоморфизм, а антиизоморфизм: $f_{AB}=f_Bf_A$.

[AD]

lofar, фишка вопроса про меры заключалась в том, что и в курсе, и в вышеупомянутой книжке произведение мер определялось как лебеговское продолжение (с полукольца $\mathfrak{M}\times\mathfrak{N}$), которое заведомо будет полной мерой, независимо от запутывающего условия про полноту исходных мер . Поэтому там была такая двухходовка. То есть впечатляет, насколько противоестественно это определение, которое даже из совсем плохих мер насильно делает полную.

Впрочем, где-то я читал, что это равносильно продолжению на минимальную $\sigma$-алгебру и последующему пополнению (в Халмоше, небось ...) (че-то не нахожу его в библиотеке ) (ну "теория меры" книжка)

Добавлено спустя 1 минуту 1 секунду:

За матрицы спасибо. Тоже в копилочку То есть для меня этот факт тоже был удивительным.

[nckg]

Могу предложить ещё одно небольшое упражнение в "копилку":
Пусть в гильбертовом пространстве $H$ есть 2 скалярных произведения -- $(\cdot,\cdot)_1$ и $(\cdot,\cdot)_2$. Доказать, что слабая сходимость в них равносильна.

P.S. Извиняюсь, если не в тему...