Я Вам помогу разобраться, показав, как Вы должны были написать. Прочитав
теорию, дальше продвинетесь сами. Ваш текст должен выглядеть так:
Код:
Найти все $a$, при которых система
$\sin x \sin y = 1/z^2 $,
$\cos x \cos y = - (x+y)^2/(a-\pi)^2$
(а лучше $\cos x \cos y = - \dfrac{(x+y)^2}{(a-\pi)^2}$),
и т.д. ... удовлетворяющее условиям $0\le y \le \pi/2$, и $z > 0$.
Получится следующее:
Цитата:
Найти все

, при которых система

,

(а лучше

),
и т.д. ... удовлетворяющее условиям

, и
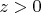
.
Если вопрос всё ещё актуален --- правьте своё сообщение.