collinear points

[ph11]

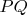
The angle bisector drawn from right-angled vertex $C$ of triangle $ABC$ intersects the circumscribed circle at point $P$, and the angle bisector from vertex $A$ intersects the circumscribed circle at point $Q$. $K$ is the intersection of line segments $PQ$ and $AB$. The centre of the inscribed circle is $O$, and its point of tangency on side $AC$ is $E$. Prove that points $E, O$ and $K$ are collinear.

[lopkityu]

Нашел следующее красивое решение

Пусть $ S $ - точка пересечения $ AB $ и $ CP $. Углы $ \angle BAQ $ и $ \angle CPQ $ опираются на равные дуги $ BQ $ и $ CQ $, потому равны, откуда $ AOKP $ - вписанный. Отсюда следует, что $ \frac{KS}{OS}=\frac{PS}{AS} $. В свою очередь, $ \frac{PS}{AS}=\frac{BS}{CS} $ и $ \triangle BCS \sim \triangle KOS $, следовательно $ KO \parallel BC $. Но, очевидно, $ OE \parallel BC $, из чего и вытекает коллинеарность точек $ K, O, E $.
P.S. С рисунком лениво было заморачиваться, т.к. не имею удобных средств рисования.

[gris]

Если позволите, вставлю картинку в знак соучастия