Киевский турнир математических боев
1 тур
21.10.2007
8–9 классы
1. Доказать утверждение: если для сторон

,

,

некоторого треугольника выполнено неравенство

, то

— наименьшая (в нестрогом смысле) сторона этого треугольника.
2. Рассматриваются все трехчлены вида

с натуральными коэффициентами, не превышающими

. Каких трехчленов больше: имеющих действительные корни, или неимеющих?
3. В треугольнике

проведены биссектрисы

и
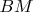
, пересекающиеся в точке

. Доказать, что если

, то

или

.
4. Пусть

. Доказать неравенство

.
5. На территории страны, имеющей форму квадрата со стороной

, находится

город. У страны есть возможность проложить

дорог. Хватит ли ей этого для того, чтобы соединить между собой все

город?
6. Правильный шестиугольник разделен на

равных треугольника. Во всех узлах образовавшейся решетки стоят разные числа. Доказать, что среди этих

треугольников разбиения найдется хотя бы

таких, в вершинах которых числа записаны в порядке возрастания против движения часовой стрелки.
7. Доказать, что число

имеет не менее

делителей.
8. В окружность вписаны треугольники

и

, при этом вершины треугольника

являются серединами дуг, на которые окружность разбивается вершинами треугольника

. В пересечении эти два треугольники образуют шестиугольник

. Доказать, что его диагонали, соединяющие противоположные вершины, параллельны сторонам треугольника

и пересекаются в одной точке.
10–11 классы
1. Пусть

, где

,

— некоторые натуральные числа. Доказать, что в равенстве можно вычеркнуть некоторые слагаемые (но не все!), чтобы оно осталось верным.
2. Существует ли такое натуральное число

, что при приписывании его к самому себе в десятичной записи выйдет точный квадрат целого числа?
3. В дом вода подается трубой, на которой установлены

кранов, каждый из которых может быть или открыт, или закрыт, причем начальное положение неизвестно. Известно, что для того, чтобы открыть воду, нужно одновременно открыть все краны. Слесарь переключает краны по одному, чтобы угадать нужное положение. Какое минимальное количество переключений ему нужно, чтобы гарантировано открыть все краны?
4. См. задачу 8 для 8–9 классов.
5. Пусть
![$[a,b,c]$ $[a,b,c]$](https://dxdy-01.korotkov.co.uk/f/c/8/4/c84b831c70dc5663fdbc7a7f02d16c4482.png)
— наименьшее общее кратное натуральных чисел

,

,

. Может ли для каких-либо натуральных чисел

,

,

оказаться, что:
![$$[x,y,z]=[x+1,y+1,z+1]=[x+2,y+2,z+2].$$ $$[x,y,z]=[x+1,y+1,z+1]=[x+2,y+2,z+2].$$](https://dxdy-01.korotkov.co.uk/f/8/e/a/8ea9b6490d34f95376ab467087e619c282.png)
6. См. задачу 6 для 8–9 классов.
7. См. задачу 7 для 8–9 классов.
8. Задан квадрат

, его пересекли полосой ширины, равной стороне квадрата. Эта полоса пересекает стороны

,

,

,

квадрата в точках

,

,

,

соответственно. Доказать, что угол между отрезками

и

составляет

.
8–9 классы
лицей «Лидер» — Сборная лицея «Престиж» и лицея №142
лицей «Наукова зміна» — лицей «Престиж»
Русановский лицей — лицей №208
лицей №142 — Украинский физико-математический лицей
Естественнонаучный лицей №145 — Технический лицей
10–11 классы
Лицей №142 — лицей «Лидер» (10 класс)
лицей «Лидер» (11 класс) — Сборная Украинского физико-математического лицея (11 класс) и лицея № 208
Технический лицей — лицей «Наукова зміна»
Украинский физико-математический лицей (10 класс) — Естественнонаучный лицей №145
Русановский лицей — лицей № 208



