
ins- писал(а):
I don't believe you.
Your beliefs is your private matter. I am not going to address them. I am ready, however, prove
my (not your) statement.
незваный гость писал(а):
If it is understood as “on the sides or their extensions”, the statement is wrong,
The operative word here is
“or their extension”. Indeed, if we are looking for the point exactly on the sides, it changes rules. We have in fact, two different problems.
~~~
Lets the
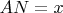
, and
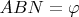
.
Lets consider the triangle
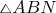
. We can write the sinus theorem for it:
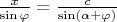
. Or,
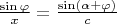
. Now, if

is the circumradius,
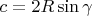
and we can write:
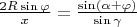
. Similar, considering other triangles we can conclude:



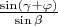
. So the problem boils down to the satisfying the last pair of equations (and, if we want points to be on sides, an additional inequality
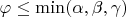
).


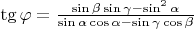
. We can express
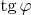
from the other equation. Obviously they have to be equal for compatibility of equations, so we have a condition on
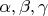
:



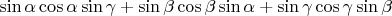
.
Phui!
Now we let
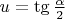
,
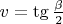
. Because
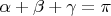
, we have an algebraic equation:






















We are looking for real positive solutions of the equation
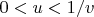
.
Well, here is graphics of the solution:

Horizontally we have

s, the red line

, green is

, and blue is

. The thin black line is

.

shows how

depends on smallest of the triangle's angles.
Obviously it demonstrates that there are solutions where points belong to sides' extensions (for example,
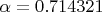
,
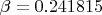
,
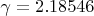
,
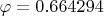
). More than, it actually demonstrates that there is no solution for “strict” sides. Before we go into discussion “graphics does not prove”, I would note that (1) there are interval calculations that prove, (2) It is easy enough to prove asymptotics near 0 (
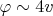
), and (3)
незваный гость писал(а):
I can neither proof nor disproof it at the moment although.
Myself, I do not see anything beautiful in this approach. May be the other one…