[Линейная алгебра] Прошу проверить решения

[nnosipov]

Ещё пара замечаний-подсказок.
Задача 1.24 стандартна, надо лишь аккуратно посчитать. Задача 1.25 не очень сложная (по-моему) и уже здесь обсуждалась.

[kp9r4d]

Подскажите, как решать 20. Я только понял, что автоморфизмы должны сохранять жорданову форму, а значит должны переводить матрицы только в подобные им, однако почему не может быть такого, что $\varphi(A) = CAC^{-1}$ и $\varphi(B) = DBD^{-1}$ и при этом $C \neq D$?

[g______d]

kp9r4d в сообщении #939970 писал(а):

почему не может быть такого, что $\varphi(A) = CAC^{-1}$ и $\varphi(B) = DBD^{-1}$ и при этом $C \neq D$?

Такое очень даже может быть. Матрицу $D$ можно умножить справа на любую обратимую матрицу, коммутирующую с $B$.

[kp9r4d]

nnosipov
Спасибо за подсказки и замечания.

Мне всё же интересна задача 20, не могу её никак которую неделю решить (решаю не круглые сутки, конечно, но всё равно довольно много времени), для начала, правильно ли я понимаю, что по изоморфизму кольца операторов однозначно восстанавливается изоморфизм, собственно, пространств?

[nnosipov]

kp9r4d в сообщении #942484 писал(а):

Мне всё же интересна задача 20

Мне тоже (только это задача 1.21). Что-то я её не понимаю. Пусть $n=1$, тогда автоморфизм сопряжения (поля комплексных чисел) даст контрпример. Нет?

[kp9r4d]

nnosipov
Вы правы, условие неверное. И не очень понятно, каким образом его можно разумным образом до верного исправить.

[patzer2097]

kp9r4d в сообщении #942749 писал(а):

И не очень понятно, каким образом его можно разумным образом до верного исправить.

Можно исправить, заменив слово "кольца" на слово "алгебры"

А еще можно исправить, пользуясь замечанием nnosipov: "Всякий автоморфизм кольца матриц имеет вид $A\to C^{-1}A^{\sigma}C$, где $C$ - какая-то невырожденная матрица, а $\sigma$ - какой-то автоморфизм основного поля". Но это, кажется, доказать сложнее. Впрочем, в Вашей задаче речь может идти о вещественных матрицах, и тогда все в порядке - все автоморфизмы $\mathbb{R}$ тривиальны.

[kp9r4d]

patzer2097
Тогда снова непонятно как доказывать. Можете ли вы дать небольшую подсказку?

[kp9r4d]

Интересно например, верно ли это:

kp9r4d в сообщении #942484 писал(а):

по изоморфизму кольца операторов однозначно восстанавливается изоморфизм, собственно, пространств

если верно, то буду уже думать в сторону того, как подобный изоморфизм построить, а как построю то там, глядишь, всё и прояснится.

[patzer2097]

kp9r4d в сообщении #943273 писал(а):

Тогда снова непонятно как доказывать. Можете ли вы дать небольшую подсказку?

Мне тоже непонятно, как это просто доказать, честно говоря. Можете здесь посмотреть не очень простое, но довольно короткое и элементарное доказательство результата (Теорема 1), из которого следует результат, указанный мной.

На самом деле, верны и другие более сильные результаты, но доказать их элементарными методами вроде бы совсем непросто.

[kp9r4d]

patzer2097
Спасибо.

[g______d]

Еще такая теорема есть.

[kp9r4d]

g______d
Спасибо. Попробую пока за неделю какое-нибудь решение, с соответствующим куском теории вывести, в качестве исследовательской задачи. Если не выведу, то хоть что-то новое узнаю, наверное.

[kp9r4d]

Пока что решил эту задачу для поля $\mathbb{F}_2$. Хотелось бы, чтобы кто-то проверил.
Будем рассматривать матрицы как линейные операторы на некотором векторном пространстве $V$ с фиксированным базисом. Пусть $f$ — изоморфизм $Mat_{n \times n}$. Докажем, что в случае, когда основное поле $\mathbb{F}_2$ существует такой изоморфизм $g$ пространства $V$, что выполняется соотношение $f(A)g(v)=g(Av), A \in Mat_{n \times n}, v \in V$. Изоморфизмы векторных пространств, как известно, являются невырожденными линейными преобразованиями, т.е. $g(v) = Bv$ для некоторого невырожденного $B$. и соотношение $f(A)g(v)=g(Av)$ будет выглядеть теперь как $f(A)Bv=BAv, v \in V$ для любого $v$. Так как $v$ любое, то операторы слева и справа тождественны, т.е. $f(A)B = BA$ и отсюда $f(A) = BAB^{-1}$.
Из свойства $f(A)g(v)=g(Av)$ следует свойство $\operatorname{Im} f(A) = g( \operatorname{Im} A)$, а из него следует, что действие $g$ на подпространствах $V$ однозначно определено, однако в случае поля $\mathbb{F}_2$ одномерные подпространства и векторы неразличимы, поэтому $g$ однозначно определяется.

[kp9r4d]

Кое-что новое узнал, но задачу не решил, буду решать дальше.
Хотелось бы, чтобы кто-то это решение проверил, потому что у меня, вроде как, получилось усилить результат задачи.
Задача 1.23
Пусть $A$ линейный оператор в пространстве $V$. Если для любого $x$ вектора $x, Ax, A^2x, ... ,A^{k-1} x$ линейно независимы, то степень минимального многочлена $A$ не больше $k$.
Решение
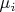
Рассмотрим сначала случай диагонализируемого $A$, перейдём в базис, в котором его матрица будет диагональной. После чего найдём (в силу линейной зависимости) для какого-нибудь вектора $v$, у которого все координаты ненулевые, такие $\mu_i$ что $(\sum\limits_{i=0}^{k-1} \mu_i A^i)v = 0$. В силу диагональности $A$ многочлен $(\sum\limits_{i=0}^{k-1} \mu_i x^i)$ будет аннулирующим вообще для любого $v$ (так как это, по сути, совокупность из $k$ равенств, в каждом из которых ненулевая координата $x$ умножается на $\sum_j \mu_j a_{ii}^j$ и всё это равно нулю), значит, степень минимального многочлена не больше, чем $k-1$. Остаётся вспомнить, что множество диагонализируемых операторов плотно в пространстве всех операторов и минимальный многочлен непрерывно от оператора зависит.