Уважаемые участники форума!
Я хотел бы задать вопрос в продолжении
этой темы. Буду благодарен за любую помощь, т. к. уже несколько месяцев "живу" этой задачей, но математической квалификации, увы, недостаточно для ее решения.
Итак, имеется следующая последовательность функций, заданных на интервале
![$x\in\left[0,1\right]$ $x\in\left[0,1\right]$](https://dxdy-04.korotkov.co.uk/f/b/a/7/ba76cb011a028a375eaf4fece260165982.png)
:

.
Необходимо доказать следующее:
Найдется такое
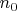
такое, что для

: у функции

все производные, начиная со второй, будут знакопеременны в точке

, т.е.:

Я действовал следующим образом:
Для начала я воспользовался представлением логарифма при помощи интеграла Фруллани, как было рекомендовано уважаемым
sup в предыдущей теме:

.
Тогда, для

:

Соответственно:

Вынося за скобки

и делая легкую перегруппировку:
![\begin{multline*}
\frac{d^k F_n(x)}{dx^k} |_{x=1} = (-1)^k(k-2)! \times\\
\times\left[ \frac{n!}{(n-k+1)!(k-2)!}\left( k\int \limits_0^{\infty}\frac {e^{-s(n-k+2)}(1-e^{-s})^{k-1}}{s}ds -(n-k+1)\int \limits_0^{\infty}\frac {e^{-s(n-k+1)}(1-e^{-s})^k}{s}ds \right) -1\right].
\end{multline*} \begin{multline*}
\frac{d^k F_n(x)}{dx^k} |_{x=1} = (-1)^k(k-2)! \times\\
\times\left[ \frac{n!}{(n-k+1)!(k-2)!}\left( k\int \limits_0^{\infty}\frac {e^{-s(n-k+2)}(1-e^{-s})^{k-1}}{s}ds -(n-k+1)\int \limits_0^{\infty}\frac {e^{-s(n-k+1)}(1-e^{-s})^k}{s}ds \right) -1\right].
\end{multline*}](https://dxdy-02.korotkov.co.uk/f/5/6/2/56256fca4d1bcff5d8dbcb03076aee5682.png)
Можно представить еще так:
![\begin{multline*}
\frac{d^k F_n(x)}{dx^k} |_{x=1} = (-1)^k(k-2)!\times\\
\times\left[ \frac{n!}{(n-k+1)!(k-2)!}\left( (n+1)\int \limits_0^{\infty}\frac {e^{-s(n+1)}(e^s-1)^{k-1}}{s}ds
-(n-k+1)\int \limits_0^{\infty}\frac {e^{-sn}(e^s-1)^{k-1}}{s}ds \right) -1\right].
\end{multline*} \begin{multline*}
\frac{d^k F_n(x)}{dx^k} |_{x=1} = (-1)^k(k-2)!\times\\
\times\left[ \frac{n!}{(n-k+1)!(k-2)!}\left( (n+1)\int \limits_0^{\infty}\frac {e^{-s(n+1)}(e^s-1)^{k-1}}{s}ds
-(n-k+1)\int \limits_0^{\infty}\frac {e^{-sn}(e^s-1)^{k-1}}{s}ds \right) -1\right].
\end{multline*}](https://dxdy-03.korotkov.co.uk/f/6/f/a/6facc20a2dcbce7b9343490eef80876082.png)
Видно, что необходимо доказать, что выражение в больших круглых скобках всегда больше, чем

. На этом месте у меня ступор. Я пробовал разные варианты:
1. В Градштейне и Рыжике есть эти интегралы из последнего выражения, но они там представляются в виде знакопеременных рядов, содержащих логарифмы и там у меня ничего не получилось (кстати, осторожно, в Советских изданиях Г-Р в этих формулах опечатка).
2. Пользуясь разложением экспоненты в ряд Маклорена:

провел интегрирование по частям для обоих интегралов в круглых скобках. Получил выражение из Градштейна и Рыжика.

3. Пользуясь неравенствами

и

оценить выражение в круглых скобках снизу. Не получилось, т.к. оценка оказалась слишком неточной.
Все портит это

в знаменателе, что с ней делать понять не могу...

Вобщем, ещё раз повторюсь, буду благодарен за любую подсказку дальнейших ходов, т.к. моя фантазия уже иссякла.
Заранее спасибо всем!



