От улитки Паскаля она отличается вот этой подчёркнутой двоечкой:

Полярное уравнение совсем не страшное, даже наоборот:

Имеется и рациональная параметризация.
Моя улитка запросто переползает с одного концентричного круга кривизны на другой, сделав при этом оборот на

(даже если общий центр ушёл в бесконечность,
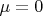
). При этом, если круги ещё и одинаково ориетнированы

, она кривизну монотонно меняет (ну, всем строителям дорог известно, что при противоположной ориентации вложенных кругов монотонной дороги не существует). Улитка Паскаля этому трюку совсем не обучена.
Параметром

можно обеспечить любое отношение радиусов (кроме равенства).
Не правда ли, хороша?
Если Вам где-то
в лесу на страницах попадалась такая улитка, сообщите, плииз.
То, что
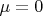
есть также частный случай эллиптической лемнискаты, я уже заметил.
Других сходств не обнаруживается.