Задача про последовательности

[arseniiv]

(Не знаю, как у неё с олимпиадностью.)

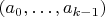
Рассмотрим конечные последовательности $(a_0, \ldots, a_{k-1})$. Окружением члена $a_i$ назовём тройку $(a_{(i-1) \bmod k}, a_i, a_{(i+1) \bmod k})$.

Найдите наибольшую длину $S$ последовательности из чисел $1,\ldots,n$, в которой все окружения разные.

Например, для 1 и 2 это $n^3$ (последовательности 1 и 11121222).

(Было бы неплохо описать алгоритм построения какого-то семейства максимальных последовательностей.)

[maxal]

Ответ всегда $n^3$. Искомая последовательность легко получается из эйлерова цикла в графе де Брёйна, вершинами которого являются двойки чисел, а ребрами - тройки. Эйлеров цикл в нём существует потому как входящая и выходящая степень каждой вершины равна $n$ (т.е. равны между собой), а граф, очевидно, связен.

[arseniiv]

Просто и красиво! Спасибо.