Задачи из номера 11
"Математического Просвещения".
1. (М.Панов) Вычислить
 2.
2. (Р.М.Травкин) Назовем
кубоидом выпуклый многогранник в трехмерном пространстве, комбинаторно эквивалентный кубу (т.е. существует взаимно однозначное соответствие между их вершиами, ребрами и гранями, сохраняющее примыкание). Рассмотрим для каждой грани точку пересечения отрезков, соединяющих середины противоположных сторон. Эти 6 точек являются вершинами некторого октаэдра. Какие значения может принимать отношение объема этого октаэдра к объему исходного кубоида?
3. (К.Шеннон)

и

-- два разбиения единичного квадрата на непересекающиеся измеримые множества.

-- пересечение множеств

и

,
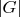
-- площадь множества

. Докажите неравенство:
 4.
4. (А.Я.Канель)

-мерная ладья бьет по прямым вдоль осей координат.
а) Какое максимальное число ладей можно расставить в

-мерном кубе

так, чтобы они не били друг друга?
Назовем расстановку ладей
полной, если в ней максимально возможное число ладей.
б) Слоем трехмерного куба

назовем квадрат

, состоящий из клеток с одинаковой третьей координатой. Пусть первые

слоев заполнены полно (т.е. в них стоят

ладьей). Докажите, что эту расстановку можно продолжить до полной расстановки всего куба. Верно ли аналогичное утверждение для четырехмерного куба?
в) В трехмерном кубе

расставили ладьи и зафиксировали угловую клетку. Рассматриваются подкубы (

, для каждого

один подкуб, всего

подкубов) с этой угловой клеткой. В каждом таком подкубе оказывается некоторое число ладей из нашей расстановки, и в некоторых подкубах расстановка оказывается полной (т.е. стоит максимально возможное число для данного

). Каково максимальное число таких подкубов с полной расстановкой? Аналогичный вопрос для

-мерного куба.
5. (М.Концевич) Hа плоскости отметили

непересекающихся отрезков и

точки, которые не лежат на этих отрезках. Докажите, что найдутся две точки, которые "видят" друг друга (т.е. соединяющий их отрезок не пересекает отмеченные отрезки).
6. (Э.Туркевич) Обозначим через

сумму цифр числа

. Ограничена ли последовательность

?
Обсуждение: topic11591.html7. (А.Я.Белов) Рассмотрим множество непрерывных функций на отрезке
![$[0,2n]$ $[0,2n]$](https://dxdy-03.korotkov.co.uk/f/6/4/3/643f28db0daaa141f6e2e5394534e41c82.png)
, таких, что

и на любом интервале

,

, производная равна

.
a) Каких функций больше: неотрицательных или таких, что

?
b) Как подсчитать число функций, таких, что

?
8. (A.Kanel-Belov, J.Kaminsky, M.Taicher) В пространстве даны две гладкие кривые

и

. Рассматривается множество

прямых

. Докажите, что если некоторая кривая

, непересекающаяся с

, пересекает каждую прямую из

, то обе кривые

и

лежат в одной плоскости.
9. (Д.Муштари) Можно ли множество рациональных точек единичной сферы раскрасить в два цвета (черный и белый) так, что если три точки отвечают концам трех ортогональных векторов, то одна из них будет черной, а две другие -- белыми?
10. (Фольклор) Пусть

-- целочисленные матрицы. Известно, что

,

. Докажите, что существует

такое, что

-- целочисленная матрица.
11. (Фольклор) Дано

грузов попарно различной массы и чашечные весы без гирь. Докажите, что за

взвешиваний можно найти
медиану (т.е. средний по массе груз).
12. (А.Белов, Г.Челноков) Двое по очереди на доске пишут многочлены от

переменных. Запрещается писать многочлен

, если:
(1)

представим в виде суммы кратных ранее написанных многочленов, т.е.

при некоторых
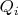
;
(2) Единица представляется в виде суммы кратных написанных многочленов и кратного

:

при некоторых
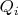
,

.
Проигрывает тот, кто не может сделать хода.
а) Докажите, что игра заканчивается.
б) Кто выигрывает при правильной игре?
Условие задачи 7.10 задачника "Математического просвещения" было сформулировано неточно. Приводим уточнение формулировки.
7.10. а) В пространстве даны две гладкие поверхности

и

, заданные уравнениями

и
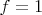
и гомеоморфные плоскости. Известно, что любую точку поверхности

можно соединить с некоторой точкой поверхности

такой ломаной длины не более

, которая находится в области

(за исключением начальной и конечной точек). Можно ли установить взаимно однозначное и взаимно непрерывное соответствие между точками

и

так, чтобы соответствующие точки находились бы на расстоянии меньше

?
б) Аналогичный вопрос для плоскости (

и

-- линии уровня функции, гомеоморфные прямой).