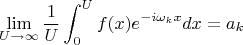маловероятно, что заинтересуется.
в рамках теории почти периодических функций задача совершенно тривиальна. пространство почти периодических функций это пополнение пространства конечных тригонометрических полиномов с произвольными наборами частот по норме, которая порождена скалярным произведением

так, что ортогональность есть и даже без кавычек.
получилось красивое такое гильбертово пространство с континуальным базисом

соответственно для решения задачи предполагалось проверить равенство