Отображения кривых

[scwec]

Пусть даны две кривые на плоскости
$1$. $E_s$: $y^2=x^3-s^2{x}$
$2$. $\tilde {E}_s$: $u^2=v^4+4s^2$.
$s$ - натуральное число.
Найдите два взаимно обратных отображения $\varphi$ : $E_s-\{(0,0)\}\to{\tilde {E}_s}$ и $\psi$ : $\tilde {E}_s\to{E_s-\{(0,0)\}}$.
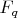
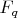
Таким способом докажите, что число $F_q$-точек на первой кривой, пополненной бесконечной точкой, больше ровно на две, чем число $F_q$- точек на второй кривой, где $q=p^r$, $p$ - простое число, не делящее $2s$,
$r$ - натуральное число.

[scwec]

Искомые отображения выглядят так: $\varphi$: $(x,y)\to{(u,v)}$, где $u=2x-\frac{y^2}{x^2}$, $v=\frac{y}{x}$ и $x\ne{0}$
$\psi$: $(u,v)\to{(x,y)}$, где $x=\frac{1}{2}(u+v^2)$ и $y=\frac{1}{2}v(u+v^2)$.
Легко проверяется, что это то, что надо.

[maxal]

Решение от мапла:

> factor( algcurves[Weierstrassform](u^2 - (v^4 + 4*s^2), v, u, t, z, Weierstrass) );

$$[{z}^{2}-4\,{t}^{3}+64\,{s}^{2}t,\quad 4\,{\frac {s \left( 2\,s-u \right) }{{v}^{2}}},\quad 32\,{\frac {{s}^{2} \left( 2\,s-u \right) }{{v}^{3}}},\quad -2\,{\frac {sz}{ \left( 4\,s-t \right) \left( 4\,s+t \right) }},\quad 2\,{\frac {s \left( {t}^{2}+16\,{s}^{2} \right) }{ \left( 4\,s-t \right) \left( 4\,s+t \right) }}]$$

Остается только поделить уравнение на $2^8$ и обозначить $y=\tfrac{z}{2^4}$ и $x=\tfrac{t}{2^2}$.

[scwec]

Да, красивый трюк. Испробовал у себя. Буду пользоваться. Спасибо.
И заодно с мнимой единицей: если будет желание, посмотрите уравнение $y^2=2x^4-1$.
Преобразование к форме Вейерштрасса без указания рациональной точки - появляется мнимая единица, с указанием рациональных точек $[1,1,1],[13,239,1]$ -её нет. Выходное уравнение - одно и то же во всех трех случаях. Формулы преобразования, конечно, разные.
Но комплексные решения исходному уравнению удовлетворяют.