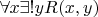Проверьте, пожалуйста несколько задач.
К первой задачи: Множество всех
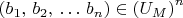
для которых
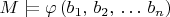
называется "definable subset of

(by

)".
Цитата:
2.12. Let
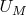
be the underlying set for structure

. Suppose that
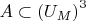
and
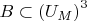
are definable subsets of
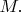
(a) Show that
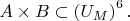
(b) Suppose we rearrange the order of the

tuples. Consider the set of all
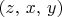
such that

is in A. Show that this set is definable.
(c) Show that
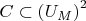
is definable where

is the set of ordered pairs
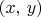
such that

is in

for some

(d) Show that
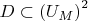
is definable where

is the set of ordered pairs
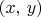
such that both
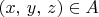
for some

and
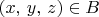
for some

(e) Show that
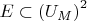
is definable where

is the set of ordered pairs
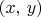
such that. for some

,

is in both

and

Пусть

и

формулы определяющие

и

, соответсвенно. Тогда мои ответы такие:
(a)
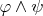
(b)
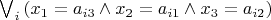
, где
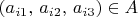
(c)
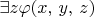
(d)
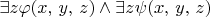
(e)
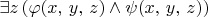
Цитата:
2.13. We define the distance
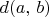
between two vertices

and

of a graph as the least number of edges in a path from

to
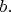
If no such path exists, then
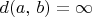
. Recall that
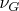
is the vocabulary of graphs.
(a) Show that, for any

, there exists a
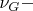
formula
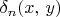
so that, for any graph

,
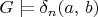
if and only if
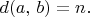
(Define the formulas
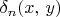
by induction on

)
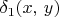
:
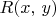
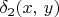
:
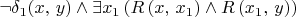

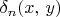
:
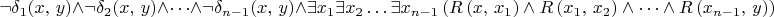
Цитата:
2.14. (a) Define a
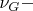
sentence

such that

has arbitrarily large finite models and, for any model

,

is a connected graph.
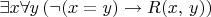
.
Цитата:
2.15. (a) Define a
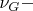
sentence

such that
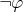
has arbitrarily large finite models and,
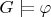
for any connected graph

.
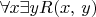
Цитата:
2.16. (a) Define a
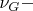
sentence

such that

has arbitrarily large finite models and, for any finite model

of

,
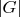
is even.