максимальная степень 2-ки делящая сумму

[maxal]

Найдите

$$\min_{m=1,2,\dots}\quad \nu_2\left( \sum_{i=0}^n \binom{n}{i} i^m \right),$$

где $\nu_2(x)$ - максимальная степень 2-ки делящая $x$.

[Руст]

Пусть $S(n,m)=\sum_{i=0}^n\binom{n}{i}i^m$. Тогда $S(n,0)=2^n$, $S(n,1)=n2^{n-1}$.
Имеет место $S(n,m)=nS(n-1,m-1)$. Поэтому $S(n,m)=n(n-1)..(n-m+1)2^{n-m},m\le n$ при $n<m, v_2(S(n,m))\ge v_2(S(n,n))=v_2(n!)$. Остается найти минимум $f(n)=min_mv_2(S(n,m))=min_mv_2(n!)-v_2((n-m)! )+n-m$.
Так как $n-m>v_2((n-m)!)$ минимум будет при $n=m$ и равен $v_2(n!)=\sum_{k\ge 1}[\frac{n}{2^k}].$

[maxal]

Руст в сообщении #514945 писал(а):

Имеет место $S(n,m)=nS(n-1,m-1)$.

Как?! Если вынести множитель $n$, то получится сумма $n\sum_{i=0}^{n} \binom{n-1}{i-1} i^{m-1}$, а это не то же самое, что $nS(n-1,m-1)$.

[Руст]

Ошибся $S(n,m)=n\sum_{k=0}^{m-1}S(n-1,k)$. Отсюда индукция снижения номера по $n$ и доказательство того, что минимумдостигается при $m=n$. Эта сумма $S(n,n)$ приводится так же к $n!$. Подробности сейчас не буду, ложусь спать.

[EtCetera]

Если не ошибаюсь, имеет место следующее рекуррентное соотношение для $S(n,m)$:

$$S(n,m)=S(n-1,m)+\sum\limits_{i=0}^m \binom{m}{i}S(n-1,i)$$

При этом $S(n,0)=2^n$ и $S(0,m)=0$, $m>0$.

(Доказательство)

При $n>0$ имеем:
\begin{multline*}S(n,m)=\sum\limits_{i=0}^n \binom{n}{i}i^m=\sum\limits_{i=0}^n \binom{n}{i}\left.\left(e^{ix}\right)^{(m)}\right|_{x=0}=\left.\left(\sum\limits_{i=0}^n \binom{n}{i}\left(e^x\right)^i\right)^{(m)}\right|_{x=0}=\\ \shoveleft{=\left.\left(\left(e^x+1\right)^n\right)^{(m)}\right|_{x=0}=\left.\left(\left(e^x+1\right)^{n-1}\right)^{(m)}\right|_{x=0}+\left.\left(e^x\left(e^x+1\right)^{n-1}\right)^{(m)}\right|_{x=0}=}\\ \shoveleft{=S(n-1,m)+\sum\limits_{i=0}^n \binom{m}{i}\left.\left(e^x\right)^{(m-i)}\right|_{x=0}\left.\left(\left(e^x+1\right)^{n-1}\right)^{(i)}\right|_{x=0}=}\\ \shoveleft{=S(n-1,m)+\sum\limits_{i=0}^n \binom{m}{i}\left.\left(\left(e^x+1\right)^{n-1}\right)^{(i)}\right|_{x=0}=S(n-1,m)+\sum\limits_{i=0}^m \binom{m}{i}S(n-1,i)}\end{multline}

[Руст]

От этого соотношения до решения далеко. То, что я писал переписав

$$i^{m-1}=\sum_{k=0}^{m-1}binom{m-1}{k}(i-1)^k$$

приводит к указанной формуле и к справедливости старого решения $v_2(S(n,m))>v_2(S(n,n)), m<n$ и $v_2(S(n,n)=v_2(n!).$

[EtCetera]

Руст

Руст в сообщении #515015 писал(а):

приводит к указанной формуле

Если под "указанной формулой" Вы имели в виду это соотношение:

Руст в сообщении #514961 писал(а):

$S(n,m)=n\sum_{k=0}^{m-1}S(n-1,k)$

то рискну заметить, что оно не верно, поскольку дает для $S(n,3)$ значение $n(n^2+n+2)\cdot 2^{n-2}$.
Правильные значения $S(n,m)$ при $0\le m\le 4$:
$S(n,0)=2^n$
$S(n,1)=n\cdot 2^{n-1}$
$S(n,2)=n(n+1)\cdot 2^{n-2}$
$S(n,3)=n^2(n+3)\cdot 2^{n-3}$
$S(n,4)=n(n+1)(n^2+5n-2)\cdot 2^{n-4}$
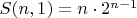
Они получены с помощью слегка измененной (для упрощения преобразований) формулы

$$S(n,m)=2S(n-1,m)+S(n,m-1)+(m-2)S(n-1,m-1)+\sum\limits_{i=0}^{m-3}\binom{m-1}{i}S(n-1,i+1)$$

Но, так или иначе, для этих значений действительно соблюдаются правила $\nu_2(S(n,n))=\nu_2(n!)$ и $\min\limits_{m=1\dots 4} \nu_2(S(n,m))=\nu_2(S(n,n))$

[Руст]

Я пропустил биномиальные коэффициенты в выражении, которые не влияют на вычисление $v_2(S(n,n))=v_2(n!).$
На самом деле:

$$S(n,m)=n\sum_{i=1}^n\binom{n-1}{i}i^{m-1}=n\sum_{i=0}^{n-1}\sum_{k=0}^{m-1}(i+1)^k=$$

$$=n\sum_{k=0}^{m-1}\sum_{i=0}^{n-1}\binom{m-1}{k}\binom{n-1}{i}i^k=n\sum_{k=0}^{m-1}\binom{m-1}{k}S(n-1,k).$$

Далее доказываем по индукции, что $v_2(S(n,m))>v_2(S(n,n))=v_2(n!), m<n, v_2(S(n,m))\ge v_2(S(n,n)),m>n,$ воспользовавшись приведенной рекурентной формулой.