С верной оговоркой насчёт "но для составных

могут быть другие".
Ближайшее нашёл в

.
Уравнение

при должных ограничениях можно переписать так:

(1).
Похожее уравнение

можно переписать как

.
Перемножая почленно выражения

и

,
получаем

, или

.
Первое выражение - известное разрешимое уравнение, второе - тождество. Если верно (1), то пара

удовлетворяет уравнению (2), и оба решения следуют из разложения

в непрерывную дробь. Уравнение из темы можно рассматривать как частный случай при

. Или такое:

. Некоторые его решения выражаются последовательностью

. Для вычислений удобно использовать схему из поста выше, но кроме самого факта разрешимости уравнения (2) отсюда мало что следует. Важнее другое: в отличии от уравнения Пелля решения уравнения (2) могут быть не единственны, что не удивительно: условия разрешимости (2) выглядят мене жесткими в сравнении с (1). Вопрос: сколько вообще существует способов представить натуральное

дробью вида

? Ответ находится быстро, если вычесть единицу из обеих частей уравнения

(3).

или

или

. Следовательно, для каждой пары

величина

определена однозначно. Решить уравнение (3), исходя из свойств

- означало бы получить сведения о делимости

. Но можно поставить другую задачу:
исходя из свойств  , найти решения (3) с наименьшими
, найти решения (3) с наименьшими 
, т.е. найти такие пары

, для которых

.
Пусть для некоторого

выполняется

. Тогда для всех

верно

, и должно выполняться

или

или

. Разлагая последнее выражение в непрерывную дробь, получаем последовательность нужных значений

, а значит и

.
Сделаем преобразования:

. В знаменателе последней дроби - целое число. Обозначив его

, получаем кв. иррациональность в приведенном виде:

Две первые дроби разложения имеют вид

, и последовательность

определена:



Переменная

- вспомогательная и нужна только для вычисления
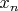
по формуле

. Попробуем получить
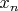
напрямую:




И так, некоторые решения уравнения (3) с наименьшими

можно получить из последовательности дробей

где

удовлетворяет условию

,

, последовательность
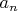
- результат разложения иррациональности

в непрерывную дробь. Алгебраическая сумма в числителе не противоречит предыдущим предложениям, привнося варианты решений. Значения

определены формулой

, а также следуют непосредственно из

-го шага самой процедуры разложения (знаменатель новой дроби после сокращения***). Для

, выбирая

в качестве

, получаем разложение

и соответствующие решения:

По сути, это некий альтернативный способ получения маленьких квадратичных вычетов по

с соответствующими квадратами, предполагающий наличие информации о делителях

. Вместо натурального

можно подставить рациональное

и провести аналогичные преобразования, обобщив заодно полученный результат: некоторые решения уравнения

с наименьшими

можно получить из последовательности дробей

где

удовлетворяет условию

,

, последовательность
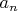
- результат разложения иррациональности

в непрерывную дробь (предполагается

). Значения

определены формулой

, а также следуют непосредственно из

-го шага самой процедуры разложения (знаменатель новой дроби после сокращения). Для пропорциональных решений, полученных таким способом, имеется ограничение: коэффициент пропорциональности

.
Можно добавить, что описанная схема легко продолжается на степени

, но если сложности, возникающие при разложении иррациональности
![$\frac{m-1}{x_0-\sqrt[k]{m}}$ $\frac{m-1}{x_0-\sqrt[k]{m}}$](https://dxdy-01.korotkov.co.uk/f/0/1/1/011e77c2c9cfd28320267cbce5c6528a82.png)
еще преодолимы, то проблема роста последовательности

сохраняется всегда.

Остаются вопросы применимости и полноты, т.е. любое ли решение может быть получено таким способом? Скорее всего нет. Тройку

, указанную
ИСН, удается получить, при

из пропорциональной дроби

. А при

что-то не видать (мало квадратов

).
Пожалуй и всё.
***
Совпадение этих последовательностей - полная для меня неожиданность. Не знаю как доказать. Может просто.


