Spook писал(а):
Профессор Снэйп писал(а):
Если интересно, могу всё расписать подробно.
Да, напишите пожалуйста, было бы очень интересно.
Линейный порядок называется
порядком без концов, если для любого

найдутся

и

, такие что

. Линейный порядок называется
плотным, если для любых

и

, таких что

, существует

, для которого

. Очевидно, что
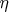
и

--- счётные плотные линейные порядки без концов.
Теорема: Все счётные плотные линейные порядки без концов изоморфны.
Доказательство. Пусть

и

--- два счётных плотных линейных порядка без концов. Покажем, что они изоморфны.
В силу счётности имеем

и

.
Частичным изоморфизмом этих порядков назовём такое конечное подмножество

множества

, что для любых

выполнено

.
Определим по индукции последовательность

частичных изоморфизмов.
1) Зафиксируем произвольные

,

и положим

.
2) Пусть

определено. Если для некоторого

справедливо

, то полагаем

. В противном случае пусть

при некотором

и

(соответственно

). Далее действуем в зависимости от того, какой из трёх нижеперечисленных случаев выполняется.
a)

. Так как второй порядок не имеет левого конца, то найдётся

, такой что

. Выберем один из таких

и положим

.
b)

. Так как второй порядок не имеет правого конца, то

для некоторого

. Выберем один из таких

и положим

.
c)

для некоторого

. Так как второй порядок плотен, то найдётся

со свойством

. Опять выберем один из таких

и положим

.
3) Пусть определено

. Действуем "симметрично" предыдущему случаю. Если для некоторого

справедливо

, то полагаем

. В противном случае пусть

при некотором

и

(соответственно

). Далее действуем в зависимости от того, какой из трёх нижеперечисленных случаев выполняется.
a)

. Так как первый порядок не имеет левого конца, то найдётся

, такой что

. Выберем одно из таких

и положим

.
b)

. Так как первый порядок не имеет правого конца, то

для некоторого

. Выберем одно из таких

и положим

.
c)

для некоторого

. Так как первый порядок плотен, то найдётся

со свойством

. Опять выберем одно из таких

и положим

.
Пусть теперь

. Легко видеть, что

--- искомый изоморфизм порядков.

Надеюсь, понятно, почему метод, используемый в конструкции из доказательства, назван "челночным". Мы по шагам мотаемся туда-сюда между двумя порядками, как челнок в швейной машинке. На нечётных шагах вида

мы прихватываем стежком элемент

первого порядка, на чётных шагах вида

--- элемент

второго порядка. В пределе мы захватываем стежками все элементы обоих порядков, сшивая их изоморфизмом

.
P. S. Про "связность"

и "несвязность"

я, честно говоря, сам не понял. Связность вроде бы топологическое понятие. Разве что речь идёт о топологии, имеющей в качестве базиса множество всех интервалов; это, конечно, корректно, но, на мой взгляд, чересчур надуманно в плане напрасного привлечения лишних сущностей. Что касается
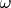
, то, как уже было замечено,

. Действительно, в

есть элемент, для которого существует бесконечно много меньших элементов, а в
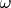
такого элемента нет.
P. P. S. В качестве упражнения докажите, что

,

и

