та матрица из линейных операторов представляет на деле один линейный оператор на парах
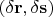
[...], так что у вас в итоге останется просто композиция таких операторов.
это понятно :) Меня больше другое волновало - как реально с такими конструкциями работать можно с целью получить простое компактное легко вычислимое выражение (ведь мне нужно будет его использовать в численных методах) - например, насколько для таких "матриц" справедливы свойства, что и для обычных (формулы перемножения, например), можно ли выносить "за скобки" и т.п.
* В смысле, действующий на сумме

пространств, где
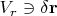
и

, и эта матрица — «разложение» его в «базисе», определяемом вложениями

и

, в том смысле, что если взять обычную матрицу для такого оператора, она будет, понятное дело, блочной и иметь аналогичный вашей вид, если базис

составить из базисов
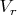
и
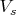
. Это всё просто на всякий случай.
ммм... Матрица оператора, насколько мне известно, сводит его действие к простому умножению, а в моем случае некая смесь "умножений" и применений операторов. Или Вы имеете в виду, что я не до конца их разложил, и потому получились "блочные формы"? Если так, то какой раздел математики такими штуками занимается? Это как-то связано с
диадиками?
(кстати, почему

, а не

?)
потому что так легче различать обычные векторы (коими являются

от дифференциалов (ака линейных приращений) векторных функций, коими являются

). Это не очень важно в простых случаях, но для более сложных все же помогает не запутаться.
Это было бы хорошо, если бы решение было единственное.
да, вроде, из физических соображений кажется, что единственное [хотя интересный вопрос к физикам :) ]. И это не сильно принципиально - можно потом "прощупать" пространство возможных решений на другие варианты.
вот это означает, что надо проверять, грубо говоря, все комбинации всех треугольников...
нет, не надо. В это и замечательность методов градиентных спусков - не надо делать перебор - нам будут указывать направление, в котором находится локальный минимум целевой функции [правда, при условии ее дифференцируемости, но в моем случае будет кусочная дифференцируемость, что, возможно, не очень все испортит])
У Вас там ошибка, кстати...
принципиальная? Если да, то подскажите, пожалуйста, в чем.
то возможно, но что это даст практически? Это никак не упростит и не ускорит вычисления и не поможет (кажется) увидеть возможные "редукции" вроде той, что продемонстрировал svv...
это как минимум поможет найти градиент :) Ведь я пока имею только нечто, способное вычислять дифференциал. А мне нужен градиент :) А для этого нужно "увидеть картину целиком" - как там из приращений аргументов получаются приращения функции по отдельным координатам.



