Нумеруем оба множества и поочерёдно подбираем соответствия элементам этих множеств в другом множестве: сначала — первому элементу первого множества, потом — первому элементу второго, потом — снова элементу первого, потом — второго, и так далее.
Ну, то есть это моя догадка
Беру элемент

. Это - аналог дроби

в дереве Штерна—Броко. Беру

. Если

, то

- аналог

. Если же

, то

- аналог

. Дальше беру такой

, что

. Смотря по соотношениям между элементами множества

, ему тоже может быть указан аналог в этом дереве.
Там я хотел продолжить так. Если для множества рациональных чисел

, таких, что

, я могу указать в другой модели множество элементов

, таких, что
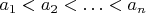
, то, какое бы рациональное число

я бы ни добавил к множеству

, во второй модели всегда можно указать такой элемент

, который соотносится с каждым элементом

множества

также, как

соотносится с

оказалась уместной? Только надо в обе стороны, да?
-- 06.03.2018, 22:38 --потом — первому элементу второго
При этом, если этот первый элемент второго оказался равен выбранному
сначала — первому элементу первого множества
, то для него назначаем первый элемент первого множества?



