Ориентация и деформация базисов

[ikozyrev]

Назовем базисы $e$ и $e'$ одинаково ориентированными если определитель матрицы перехода $C_{e\to e'}$ - положителен.
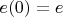
Назовем непрерывной деформацией базиса $e$ такое семейство базисов $e(t)$ зависящее от параметра $t\in [0,1]$ что $e(0)=e$ и коэффициенты матрицы перехода непрерывно зависят от $t$.
Доказать, что базисы $e$ и $e'$ одинаково ориентированны тогда и только тогда, когда существует непрерывная деформация $e(t)$ такая что $e(1)=e'$.
В одну строну легко - пусть у нас такая деформация существует, тогда определитель матрицы перехода - это многочлен от коэффициентов матрицы перехода, а значит он является непрерывной функцией от $t$, а значит если $detC(0)>0$ и $detC(1)<0$ то где-то она принимает нулевое значение, что противоречит определению деформации.

А вот в обратную строну - затык.
Пусть у нас базисы одинаково ориентированы. Тогда нам надо построить такую непрерывную деформацию, чтобы она принимала значение $e'$ в единице.
Первое что приходит в голову - определить такую деформацию непосредственно на коэффициентах матрицы перехода.
То есть мы имеем матрицу перехода $C_{e\to e'}$ в точке 1 с положительным определителем, а также единичную матрицу перехода в точке 0.
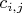
Тогда для каждого коэффициента матрицы $c_{i,j}$ определим функцию $c_{i,j}(t)$ непрерывную на отрезке $[0,1]$ как линейную функцию со значениями $c_{i,j}(t)=\delta_{i,j}$ и $c_{i,j}(1)=c_{i,j}$. Тогда получим искомую непрерывную деформацию. Но как доказать что определитель данной матрицы нигде на отрезке $[0,1]$ не обращается в ноль?

[Xaositect]

А он может обращаться в ноль, можно, например, взять в двумерном пространстве $e'_1 = -e_1$, $e'_2 = -e_2$.

Попробуйте разложить матрицу перехода в какое-нибудь произведение, чтобы для каждого сомножителя можно было просто построить удобную деформацию.

[ikozyrev]

Ортогональную на верхнетреунольную? Для верхнетреунольной деформация строится а как для ортогональной?

[Xaositect]

Ортогональная матрица есть композиция поворотов.

[ikozyrev]

Xaositect в сообщении #1261432 писал(а):

Ортогональная матрица есть композиция поворотов.

Я тоже об этом подумал...но ведь повороты могут быть только в евелидовом пространстве? А у нас тут на евклидовость ограничение не накладывается...

[Xaositect]

Ну, если мы говорим об ортогональных матрицах, мы уже в некотором смысле говорим о евклидовом пространстве.
Но его можно не упоминать. Ортогональная матрица есть произведение матриц поворота.

[ikozyrev]

Xaositect в сообщении #1261496 писал(а):

Ну, если мы говорим об ортогональных матрицах, мы уже в некотором смысле говорим о евклидовом пространстве.
Но его можно не упоминать. Ортогональная матрица есть произведение матриц поворота.

Спасибо, с этим понятно.
То есть делаем так: исходная матрица $C_{e\to e'}$ с положительным определителем разлагается в произведение $C_{e\to e'}=QR$, где $Q$- ортогональная а $R$ - верхнетреугольная, обе с положительными определителями.
$Q$ - композиция поворотов, поэтому можно сделать нерерывную деформацию из единичной в нее, а деформацию из $E$ в $R$ делаем линейным способом, а так как на главной диагонали у нее можно сделать все коэффициенты положительными, то определитель при такой деформации в ноль не обращается, так?

[Xaositect]

Да, так работает.

Либо еще можно напрямую через действительную жорданову форму.

[ikozyrev]

Xaositect в сообщении #1261523 писал(а):

Да, так работает.

Либо еще можно напрямую через действительную жорданову форму.

Спасибо!