Наверно вероятностное пространство с равными вероятностями исходов для данной задачи не подходит. Надо по-другому. Прав ли я?
Пусть имеется некоторая арифметическая функция

, принимающая значения:

соответственно с вероятностями

.
Предположим, что существуют пределы:

,

.
Тогда предельным распределением для

будет распределение

.
ДоказательствоВ каждой точке натурального ряда

мы задаем вероятностное пространство

, где

,

- все подмножества

,

, где

.
Введем последовательность случайных величин на данном вероятностном пространстве

которая принимает значения из

с вероятностями из

.
Тогда функции распределения указанных случайных величин имеют вид:
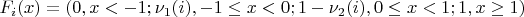
.
На основании (Замечания 4 на стр 123 Боровков "Теория вероятностей") функции распределения

сходятся к

, как дискретные распределения, имеющие скачки в одних и тех же точках.
Вы не ответили на вопрос: зависят ли вероятности

от

?
Значение

пробегает значение до

, если

стремится к бесконечности, то

пробегает весь натуральный ряд.



