Продолжение задачи. Просьба проверить.
Пусть последовательность случайных величин

слабо сходится к случайной величине

.
Вычислим математическое ожидание и дисперсию случайной величины

:

. (1)
Необходимо определить предельную функцию распределения для случайной величины

, где

- случайная величина, рассмотренная в первой части задачи.
Решение
Случайную величину

можно представить в виде:

.(2)
На основании (2)

является цепью Маркова.
Учитывая, что вероятности

зависят от

, то

является неоднородной цепью Маркова с конечным

числом состояний.
В каждое следующее состояние данная цепь переходит с вероятностью

, в предыдущее состояние - с вероятностью

и остается в том же состоянии с вероятностью -
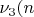
(3).
При

значения:

. (4)
На основании (4) при

случайная величина

слабо сходится к случайной величине

:

. (5)
Случайная величина

представляет из себя простое случайное блуждание со счетным числом состояний. Начальное значение данного случайного блуждания

.
На основании (4) вероятность перехода в следующее состояние у данного случайного блуждания равна

, вероятность возврата в предыдущее состояние также равна

, вероятность остаться в том же состоянии равна

. (6)
На основании (1), (6) математическое ожидание случайной величины

равно:

, (7) поэтому это симметричное случайное блуждание.
Бесконечное симметричное случайное блуждание имеет нормальную функцию распределения с математическим ожиданием, на основании (7), равным 0 и среднеквадратичным отклонением, на основании (1), (6):

. (8)
Слабая сходимость (5) эквивалентна сходимости по распределению.
Обозначим распределение случайной величины

-

, тогда сказанное можно записать в виде сходимости по распределению:

. (9)
Пусть арифметическая функция

, где арифметическая функция

рассматривалась в первой части задачи.
Тогда выражение (9) можно записать в виде:

, (10)
где

- функция стандартного нормального распределения.



