Не получается найти ошибку в своих рассуждениях

[Denis Kulikov]

Я знаю, что приведенное мною решение неверно. Я также знаю, как получить верное решение, но считаю лишним приводить его здесь. Я лишь хочу, чтобы вы помогли мне понять, почему приведенное мною решение неверно (где я допустил ошибку или ошибки в своих рассуждениях).

Задача.
Найдите наибольшее и наименьшее значения выражения $2a + ab$, если $-16 \leqslant a \leqslant -5$; $-12 \leqslant b \leqslant -4$.

Решение.
Воспользуемся дистрибутивным законом умножения и перепишем выражение $2a + ab$ в виде $a(2 + b)$.
Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство. Таким образом

$-12 + 2 \leqslant 2 + b \leqslant -4 + 2$;
$-10 \leqslant 2 + b \leqslant -2$.

Для того, чтобы перемножить верные неравенства одного знака, необходимо, чтобы левые и правые части неравенств были положительными числами. Умножим каждое двойное неравенство на $-1$, не забыв при этом изменить знак неравенства на противоположный:

$(-1)(-16) \geqslant -a \geqslant (-1)(-5) $;
$5 \leqslant -a \leqslant 16$;

$(-1)(-10) \geqslant (-1)(2 + b) \geqslant (-1)(-2)$;
$2 \leqslant -2 - b \leqslant 10$.

Теперь мы можем перемножить полученные неравенства:

$5\cdot 2 \leqslant -a(-2 - b) \leqslant 16\cdot 10$;
$10 \leqslant -a\cdot -2 + -a\cdot -b \leqslant 160$.

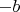
По условию, $a$ и $b$ - отрицательные числа, тогда $-a$ и $-b$ - положительные числа. Отсюда следует, что $-a\cdot -2$ - это отрицательное число, и если мы уберем отрицательный знак у каждого из множителей, то знак произведения по прежнему будет отрицательным, поэтому $-2\cdot -a = 2a$. Аналогично рассуждая, мы придем к выводу, что $-a\cdot -b = ab$. Таким образом мы получим, что $10 \leqslant 2a + ab \leqslant 160$. Из данного неравенства видно, что наименьшее значение данного выражения равно $10$, в то время как наибольшее значение равно $160$.

Докажем, что если $-16 \leqslant a \leqslant -5$ и $-12 \leqslant b \leqslant -4$, то значение выражения $2a + ab > 0$.

Доказательство.

Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство. Прибавим к обеим частям неравенства $2a + ab > 0$ число $-2a$:

$2a + (-2a) + ab > 0 + (-2a)$;
$ab >-2a$.

Если обе части верного неравенства умножить на отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство. Умножим обе части неравенства $ab > -2a$ на $\frac{1}{a}$. Так как по условию $a$ - отрицательное число, необходимо будет изменить знак неравенства на противоположный.

$\frac{1}{a}ab < \frac{1}{a}(-2)a$;
$b < -2$.

Таким образом, чтобы неравенство $2a + ab > 0$ было верным, необходимо, чтобы $b < -2$. Но по условию $b$ всегда меньше $-2$, следовательно неравенство $2a + ab > 0$ является верным при любых значениях переменных $a$ и $b$. $\qed$

[Mikhail_K]

Это очень странный текст.

Во-первых, ответ у Вас получен-таки верный: минимальное значение $10$, максимальное $160$.

Во-вторых, вот эти рассуждения

Denis Kulikov в сообщении #1238784 писал(а):

По условию, $a$ и $b$ - отрицательные числа, тогда $-a$ и $-b$ - положительные числа. Отсюда следует, что $-a\cdot -2$ - это отрицательное число, и если мы уберем отрицательный знак у каждого из множителей, то знак произведения по прежнему будет отрицательным, поэтому $-2\cdot -a = 2a$. Аналогично рассуждая, мы придем к выводу, что $-a\cdot -b = ab$.

- излишни. Равенства $(-2)(-a)=2a$, $(-a)(-b)=ab$ справедливы всегда, вне зависимости от знаков множителей. Сюрприз?

В-третьих, после того как Вы перемножили неравенства и получили $10\leq 2a+ab\leq 160$, это ещё не доказывает, что минимальное значение $10$, а максимальное $160$. Это означает только то, что при любых $a$ и $b$ полученное двойное неравенство обязательно справедливо - но при этом не доказано, достигаются ли грани $10$ и $160$. Поэтому надо бы привести пример таких $a$ и $b$, для которых $2a+ab=10$ и для которых $2a+ab=160$. Тогда будет доказано, что минимальное значение $10$, максимальное $160$. Придумать эти примеры очень просто.

В-четвёртых, совершенно непонятно, зачем Вам понадобилось доказывать, что $2a+ab>0$, если Вы уже доказали, что $10\leq 2a+ab\leq 160$. Если что-то больше или равно $10$, то оно точно больше нуля. Непонятно также, как утверждение $2a+ab>0$ (безусловно верное) приближает Вас к ответу на вопрос задачи. Логика в доказательстве тоже слегка хромает, но это уже устранимо и непринципиально.

[Xaositect]

Решение по сути верное, но записано ужасно и пропущена одна важная деталь.

Denis Kulikov в сообщении #1238784 писал(а):

По условию, $a$ и $b$ - отрицательные числа, тогда $-a$ и $-b$ - положительные числа. Отсюда следует, что $-a\cdot -2$ - это отрицательное число, и если мы уберем отрицательный знак у каждого из множителей, то знак произведения по прежнему будет отрицательным, поэтому $-2\cdot -a = 2a$. Аналогично рассуждая, мы придем к выводу, что $-a\cdot -b = ab$.

Это совершенно непонятное рассуждение, тут просто надо воспользоваться тем, что $(-x)(-y) = xy$.

При этом раскрывать скобки и потом обратно собирать их совершенно не нужно, надо просто сказать, что $(-a)(-2-b) = (-a)(-(2+b)) = a(2+b)$.

Denis Kulikov в сообщении #1238784 писал(а):

Из данного неравенства видно, что наименьшее значение данного выражения равно $10$, в то время как наибольшее значение равно $160$.

А вот тут - неверный переход. Пока Вы только доказали, что $10 \leq 2a + ab \leq 160$, но из этого никак не следует, что крайние значения $10$ и $160$ на деле достигаются. Надо привести значения $a,b$, при которых $2a+ab$ действительно равно $10$ и $160$.

Denis Kulikov в сообщении #1238784 писал(а):

Докажем, что если $-16 \leqslant a \leqslant -5$ и $-12 \leqslant b \leqslant -4$, то значение выражения $2a + ab > 0$.

Это не нужно, мы уже доказали, что при этих ограничениях $2a + ab \geq 10$.

[Denis Kulikov]

Цитата:

Во-первых, ответ у Вас получен-таки верный: минимальное значение $10$, максимальное $160$.

В ответе к задаче указаны другие числа: $-12$ и $182$, что ввело меня в заблуждение. Поэтому я привел доказательство того, что $2a + ab > 0$.

Цитата:

Во-вторых, вот эти рассуждения излишни. Равенства $(-2)(-a)=2a$, $(-a)(-b)=ab$ справедливы всегда, вне зависимости от знаков множителей. Сюрприз?

Согласен.

Цитата:

В-третьих, после того как Вы перемножили неравенства и получили $10\leq 2a+ab\leq 160$, это ещё не доказывает, что минимальное значение $10$, а максимальное $160$. Это означает только то, что при любых $a$ и $b$ полученное двойное неравенство обязательно справедливо - но при этом не доказано, достигаются ли грани $10$ и $160$. Поэтому надо бы привести пример таких $a$ и $b$, для которых $2a+ab=10$ и для которых $2a+ab=160$. Тогда будет доказано, что минимальное значение $10$, максимальное $160$. Придумать эти примеры очень просто.

Я, честно, этого не знал. Очень ценное замечание. Спасибо!

Цитата:

Логика в доказательстве тоже слегка хромает, но это уже устранимо и непринципиально.

Я был бы Вам благодарен, если бы Вы указали на слабые места и помогли бы их устранить. Мне не у кого просить совета, поэтому вся надежда на этот замечательный форум.

[Mikhail_K]

Denis Kulikov в сообщении #1238797 писал(а):

Я, честно, этого не знал. Очень ценное замечание. Спасибо!

Ну, вот простой пример на эту тему.
Пусть величина $a$ принимает значения из $[0,1]$.
Тогда имеем: $0\leq a\leq 1$, $0\leq 1-a\leq 1$ (понятно откуда это?) $\Rightarrow$ $0\cdot 0\leq a(1-a)\leq 1\cdot 1$ $\Rightarrow$ $0\leq a(1-a)\leq 1$.
Последнее неравенство действительно верно для всех $a\in [0,1]$. Однако неверно, что $1$ - максимальное значение выражения $a(1-a)$ при $a\in[0,1]$. Легко показать (сделайте это!) что минимальное значение тут действительно нуль, а вот максимальное $1/4$. Понятно, что раз $a(1-a)$ не превышает значения $1/4$, то тем более не превышает и единицу, так что противоречия здесь нет.

Denis Kulikov в сообщении #1238797 писал(а):

Я был бы Вам благодарен, если бы Вы указали на слабые места и помогли бы их устранить.

Вначале Вы пишете, что собираетесь что-то прибавить к двум частям верного неравенства (и производите это). Это значит, что Вы считаете неравенство $2a+ab>0$ верным, и делаете из него выводы. В конце Вы получаете вывод $b<-2$. Итак, Вы доказали, что из $2a+ab>0$ (при выполнении ещё условия на $a$, которым Вы пользовались) следует, что $b<-2$. Вы даже правильно сформулировали этот факт: чтобы неравенство $2a+ab>0$ было верным, необходимо, чтобы $b<-2$.
Беда в том, что "необходимо" - не значит достаточно. Вы НЕ доказали, что при любом $b<-2$ Ваше неравенство будет верным. Вы доказали обратное утверждение: если неравенство верно, то обязательно $b<-2$.

То есть доказывать-то Вам нужно было в другом направлении: из $a<0$ и $b<-2$ выводить, что $2a+ab>0$.

Но я сказал, что конкретно здесь эта придирка несущественна (хотя в других случаях может быть существенной и может приводить к неверным ответам). Несущественна она здесь потому, что на каждом шаге доказательства у Вас справедливо не только прямое следование $\Rightarrow$, но и обратное $\Leftarrow$, т.е. $\Leftrightarrow$. Проверьте каждый шаг доказательства: действительно ли следование работает в обе стороны. Если Вы это понимаете, то можно доказательство никак не изменять. Разве что вместо

Denis Kulikov в сообщении #1238784 писал(а):

Таким образом, чтобы неравенство $2a + ab > 0$ было верным, необходимо, чтобы $b < -2$

написать "необходимо и достаточно". (А ещё лучше в скобках приписать: при условии $a<0$.)

[Denis Kulikov]

Mikhail_K в сообщении #1238817 писал(а):

Ну, вот простой пример на эту тему.
Пусть величина $a$ принимает значения из $[0,1]$.
Тогда имеем: $0\leq a\leq 1$, $0\leq 1-a\leq 1$ (понятно откуда это?)

$0 \leqslant a \leqslant 1 \Rightarrow -1 \leqslant -a \leqslant 0 \Rightarrow 0 \leqslant 1 - a \leqslant 1.$
Более того, мы могли бы точно также доказать, что если $0 \leqslant a \leqslant n$ - верное неравенство, то $0 \leqslant n - a \leqslant n$ - тоже верное неравенство.

Mikhail_K в сообщении #1238817 писал(а):

Легко показать (сделайте это!) что минимальное значение тут действительно нуль

Ноль достигается при $a = 0$ или $a = 1$. $\dfrac{1}{4}$ достигается при $a = \frac{1}{2}$. Более того, предположу, что если $0 \leqslant a \leqslant n$ и $0 \leqslant n - a \leqslant n$ - верные неравенства, то $0 \leqslant a(n - a) \leqslant \dfrac{n^2}{4}$ - тоже верное неравенство, но я пока не могу это доказать.

Вопрос.
Но если у меня не получается найти такие значения переменной или переменных, при которых та или иная грань достигалась бы, то как тогда быть? Как же отыскать наибольшее и наименьшее значение в таком случае?

Что касается доказательства, то я понял, что с пониманием необходимости и достаточности у меня есть проблемы. Попробую разобраться и изменить доказательство.

[Mikhail_K]

Denis Kulikov в сообщении #1238939 писал(а):

Но если у меня не получается найти такие значения переменной или переменных, при которых та или иная грань достигалась бы, то как тогда быть? Как же отыскать наибольшее и наименьшее значение в таком случае?

Производные проходили уже? Если выражение, у которого надо найти максимальные и минимальные значения, зависит от одной переменной - то в общем случае это делается с помощью производных, материал за 10-й или 11-й класс. Если переменных несколько - вот как у Вас $a$, $b$ - то это вузовский курс.
А иначе - действительно, придётся что-то угадывать, подбирать.

Ну, можно ещё доказать (подумайте, как это сделать! - заодно Вы устраните и пробел в своём доказательстве тоже), что если $f(a)$ принимает минимальное значение $f_{\min}\geq 0$ и максимальное значение $f_{\max}$, а $g(b)$ принимает минимальное значение $g_{\min}\geq 0$ и максимальное $g_{\max}$, то $f(a)g(b)$ будет принимать минимальное значение $f_{\min}g_{\min}$ и максимальное значение $f_{\max}g_{\max}$. Тут главное, чтобы функции $f$ и $g$ зависели от разных переменных - одна от $a$, другая от $b$. Ну и, конечно, чтобы все значения были неотрицательными.

Denis Kulikov в сообщении #1238939 писал(а):

Ноль достигается при $a = 0$ или $a = 1$. $\dfrac{1}{4}$ достигается при $a = \frac{1}{2}$.

Итак, примеры Вы подобрали; то, что $a(1-a)\geq 0$ при любом $a\in[0,1]$, Вы доказывать умеете. Вам осталось доказать, что

$$ a(1-a)\leq 1/4\quad \forall a\in[0,1]. $$

Перенесите здесь всё в одну часть, раскройте скобки и подумайте.
Кстати, Вы в каком классе сейчас?