Открытые и замкнутые множества на прямой (Давидович)

[grizzly]

irod
Всё-таки нет. У нас нет никакой теоремы о системе вложенных отрезков с проколотыми точками. Хотите, попытайтесь доказать (я не рекомендую).

Есть более простой путь удалять по одной точки множества. Вот есть первая точка в нашем счётном множестве $x_1$. Вы же запросто можете построить первый отрезок так, что он вообще не содержит точку $x_1=x_{n_1}$, но содержит какую-то другую точку $M$, скажем $x_{n_2}$? Что мешает Вам построить внутри этого отрезка ещё один отрезок, который бы не содержал точку $x_{n_2}$, но содержал бы другую точку $M$? И так далее.

Если понятно, как это сделать, попытайтесь всё повторить ещё раз.

[irod]

deep down в сообщении #1248734 писал(а):

Ещё найдите плотное $A\subset\mathbb{Q}$ такое, что $\mathbb{Q}\setminus A$ тоже плотно.

deep down в сообщении #1249792 писал(а):

irod в сообщении #1249725 писал(а):

Множество $\mathbb{Q}$ счетно. Пронумеруем все его элементы, и пусть $A$ -- элементы с четными номерами в нашей нумерации. Тогда и $A$ и $\mathbb{Q}\setminus A$ всюду плотные.

При нумерации получилось так, что у все положительных чисел чётные индексы, у всех отрицательных - нечётные. В результате имеем два множества, не являющихся всюду плотными.
В случае $\mathbb{Q}$ конкретный пример строится явно, и не один.

Тогда такой пример: берем $A$ состоящим из всех дробей, где числитель четный, а знаменатель нечетный (или наоборот).

[deep down]

irod в сообщении #1251549 писал(а):

берем $A$ состоящим из всех дробей, где числитель четный, а знаменатель нечетный (или наоборот).

Да, именно этот пример я и имел в виду. Похожий вариант - $A$ состоит из дробей, знаменатель которых является степенью двойки.
Утверждение, кстати, верно для любого всюду плотного, не только $\mathbb{Q}$. Доказывается просто, но зацикливаться на этом не стоит.
Вот ещё примеры всюду плотных. Надоест думать на эту тему - посмотрите

(Оффтоп)

$\{q\cdot\sqrt{2}|q\in\mathbb{Q}\}$, $(\mathbb{R}\setminus\mathbb{Q})\cup [0,1]$

И небольшое пояснение к советам grizzly. Вам нужно построить систему вложенных интервалов $I_1\supset I_2 \supset I_3\supset \dots$, чтобы точки $x_1,\dots,x_n$ не содержались в отрезке $I_n$.

[irod]

Всегда сложно добивать уже почти законченное

grizzly в сообщении #1251547 писал(а):

Если понятно, как это сделать, попытайтесь всё повторить ещё раз.

Ну собственно Вы почти все написали, осталось только красоту навести. Итак, 3-я попытка.

Задача 23*.
Может ли совершенное множество быть счетным?
Ответ.
Нет, совершенное множество либо конечно (пусто), либо несчетно.
Доказательство.
Пустое множество является совершенным и не является счетным.
Пусть теперь $M$ -- непустое совершенное множество, и пусть $U_\varepsilon(x)$ -- некоторая окрестность произвольной точки $x\in M$. Предположим, что существует $x_n=x_1,x_2,\ldots$ -- (счетная) последовательность всех точек множества $M\cap U_\varepsilon(x)$.
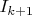
Построим внутри $U_\varepsilon(x)$ систему вложенных отрезков следующим образом. Берем первый отрезок $I_1$ так, чтобы он не содержал точку $x_1=x_{n_1}$, но содержал какую-то другую точку $M$. Далее на каждом ($(k+1)$-м) шаге берем отрезок $I_{k+1}$ так, чтобы он был минимум вдвое меньше $I_k$, не содержал $x_{n_{k+1}}$ -- точку с минимальным номером из $I_k\cap (x_n)$, но содержал бы другую точку $M$. Получим такую систему вложенных отрезков $I_1\supset I_2\supset\dots$, что точки $x_1,\dots,x_n$ не содержатся в отрезке $I_n$. Пересечением этой системы будет точка из $M$, отсутствующая в нашей исходной нумерации $(x_n)$.
Полученное противоречие доказывает что $M$ несчетно.

-- 06.10.2017, 13:43 --

Напишите пожалуйста, правильно ли мое исправленное доказательство 14-й задачи с предыдущей страницы?

(Вот оно)

irod в сообщении #1249481 писал(а):

Разберусь с еще одним долгом.

irod в сообщении #1238586 писал(а):

Задача 14.
Какие множества являются открытыми и замкнутыми одновременно?

grizzly в сообщении #1241078 писал(а):

у Вас в той задаче нет целостного рассуждения -- от условия задачи, через определения и теоремы / другие задачи, к выводу. У Вас там интуитивное рассуждение, которое не выглядит убедительным.

Пути, как это исправить, Вам предложили -- и ewert и я (лучше всё же идти по пути ewert -- он короче и естественней).

ewert в сообщении #1238731 писал(а):

Проще не ссылаться на ту задачу, а повторить ключевую часть её доказательства. Берём любую точку открытого множества и строим для неё максимальный интервал. Что можно сказать про его концы?...

Из отсутствия точек у пустого множества следуют его открытость и замкнутость.
Открытое множество $\mathbb{R}$ является замкнутым.
Пусть теперь $M\ne\mathbb{R}$ -- непустое открытое множество. Возьмем произвольную точку $x\in M$ и построим для нее максимальный интервал, входящий в $M$. Концы этого интервала есть предельные точки $M$, и следовательно должны принадлежать $M$, чтобы оно было замкнутым. В то же время концы интервала не являются его внутренними точками, следовательно их принадлежность $M$ противоречит открытости $M$. Следовательно, любое непустое открытое множество, не равное $\mathbb{R}$, не является замкнутым.
Ничего не забыл?

[grizzly]

irod в сообщении #1253680 писал(а):

Ну собственно Вы почти все написали

Нет, не всё! Если Вы построите неправильно первый отрезок в СВО, второй не факт что получится построить. Вы должны понять, почему. Придумайте пример, в котором после неудачного выбора первого отрезка нельзя будет выбрать второй по Вашему алгоритму.

Ещё замечания помельче:
1) Вы проводите доказательство от противного. В этом случае лучше объявить об этом в самом начале: "Пусть теперь $M$ -- непустое совершенное множество. Предположим от противного, что оно счётно."
2)

irod в сообщении #1253680 писал(а):

Предположим, что существует $x_n=x_1,x_2,\ldots$ -- (счетная) последовательность всех точек множества $M\cap U_\varepsilon(x)$.

Это не предположение. Это следствие из того, что $x$ -- предельная точка и что $M$ -- счётно.

По поводу задачи 14. С моей точки зрения понятие "максимальный интервал" не настолько очевидно, чтобы оперировать им на уровне одной интуиции. Я бы ожидал увидеть, что оно основано на чуть более формальных обозначениях типа: $\sup \{y : [x,y]\subset M\}$ (и зеркально в другую сторону). Тогда бы Вы не допустили такой неточности:

irod в сообщении #1253680 писал(а):

Концы этого интервала есть предельные точки $M$, и следовательно должны принадлежать $M$

Я имею в виду, что если этот интервал -- луч, то одного из концов (в Вашем понимании) у него не будет.

[irod]

grizzly в сообщении #1253698 писал(а):

Нет, не всё! Если Вы построите неправильно первый отрезок в СВО, второй не факт что получится построить. Вы должны понять, почему. Придумайте пример, в котором после неудачного выбора первого отрезка нельзя будет выбрать второй по Вашему алгоритму.

Кажется догадался.
Допустим, нам надо построить с.в.о. внутри интервала $(0,10)$. Пусть наша последовательность $(x_n)$ монотонна, например $x_1=0.1<x_2=1<x_3<\dots$. Если мы возьмем отрезок $I_1=[0.2;1]$, то он конечно будет содержать точку $x_2=1$, но только ее одну, и дальше мы никаких отрезков внутри $I_1$ не построим. Верно?

-- 06.10.2017, 16:47 --

grizzly в сообщении #1253698 писал(а):

Ещё замечания помельче:

Ок

[grizzly]

irod в сообщении #1253733 писал(а):

Верно?

Идею уловили правильно. В этот пример нужно бы ещё добавить точек между 0 и 0.1 (чтобы точка $x_1$ была предельной), но это уже мелочи.

Этот пробел доказательства исправить несложно. Но я пока не буду подсказывать.

[irod]

irod в сообщении #1253680 писал(а):

Берем первый отрезок $I_1$ так, чтобы он не содержал точку $x_1=x_{n_1}$, но содержал какую-то другую точку $M$.

Помимо своих границ, если они принадлежат $M$ (тем самым гарантируется, что это будет не единственная точка из $M$ в отрезке).

[grizzly]

irod в сообщении #1253855 писал(а):

Помимо своих границ, если они принадлежат $M$

Да. Для однотипности можно всегда брать границы отрезков, не лежащие в $M$.

(Оффтоп)

Ещё более формально можно свести к принципу пустого чайника*. Но это уже занудство, так что расшифровывать не буду, а анекдот я набрал и удалять теперь жалко :)
____

*Как будут решать задачу "Как вскипятить чайник?" физики и математики: налить воду, зажечь огонь, поставить чайник на огонь и греть до кипения.

А теперь новая задача "Как вскипятить наполненный водой чайник?"
Физики: зажечь огонь, поставить, нагреть.
Математики: вылить воду из чайника и имеем уже решённую задачу.

[irod]

grizzly

grizzly в сообщении #1253698 писал(а):

По поводу задачи 14.

Ок, тут все ясно.

Листок закончен, большое спасибо grizzly, ewert, deep down и всем остальным за помощь!
Перехожу к следующему листку - по свойствам и графикам функций.