Задача из теории чисел

[Noct]

Есть задача
доказать что при любом нечетном простом $p$, числитель числа $1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{p-1}$ делится на $p$, при этом говорят что нужно воспользоваться следующими задачами:
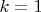
1) Пусть $p$ - некоторое простое нечетное число. Если $k \in \{1,2,\dots,p-1\}$, то показать что существует единственное $b_k$ в этом множестве, что для которого $k b_k \equiv 1 \mod p$. Показать, что $k \ne b_k$ за исключением случаев, когда $k = 1$ или $k=p-1$
2) Теорема Вильсона. $(p-1)! \equiv -1 \mod p$
Я решил задачу так:
Пусть $K = НОК(1,2,\dots,p-1)$ и $p \nmid K$

$$1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{p-1} = \frac{K + \frac{1}{2}K + \frac{1}{3}K + \cdots + \frac{1}{p-1}K}{K}$$

Докажем, что множество $\{K, \frac{1}{2} K, \dots, \frac{1}{p-1} K \}$ - образуют полную систему вычетов по модулю $p$.
Пусть $\frac{1}{n} K \equiv \frac{1}{m} K \mod p $, тогда
$m K \equiv n K \mod p $, $m \equiv n\mod p$, а множество $\{1,2,\dots,p-1\}$ - ПСВ.
Далее

$$\sum\limits_{n=1}^{p-1} \frac{1}{n}K \equiv \sum\limits_{n=1}^{p-1} \n \equiv \frac{p (p-1)}{2} \equiv 0 \mod p$$

Задачей 1 мы пользуемся чтобы перейти от $\frac{1}{n} K \equiv \frac{1}{m} K \mod p $ к $m K \equiv n K \mod p $. А где мы пользуемся Теоремой Вильсона?

[DeBill]

Noct
Про 1): Заметим для начала, что если числу $k$ соответствует $b_k$, то и, обратно, числу $b_k$ соответствует $k$ (единственность обратного). Это сразу дает, что разным $k$ соответствуют разные $b_k$ - по единственности (фактически, Вы это и проверяли с Вашим $K$). Поэтому список обратных величин совпадает со списком всех ПСВ.
(Это чуть упрощает Ваше решение)

Noct в сообщении #1229577 писал(а):

А где мы пользуемся Теоремой Вильсона?

Да нигде. Однако, нельзя сказать, что она здесь совсем не при чем: вторая фраза из 1) фактически даёт её доказательство!

[Sonic86]

Вместо загадочных $b_k$ лучше прямо писать $k^{-1}\pmod p$.

Кстати верен более общий факт: $\sum\limits_{k=1}^{p-1}k^{-1}\equiv 0\pmod {p^2}$.

[Noct]

Sonic86 в сообщении #1229614 писал(а):

Кстати верен более общий факт: $\sum\limits_{k=1}^{p-1}k^{-1}\equiv 0\pmod {p^2}$.

Интересно, а какова идея доказательства этой формулы?

[Padawan]

Sonic86 в сообщении #1229614 писал(а):

Кстати верен более общий факт: $\sum\limits_{k=1}^{p-1}k^{-1}\equiv 0\pmod {p^2}$.

Хм, $k\mapsto k^{-1}$ есть биекция $\mathbb Z/p\mathbb Z$ на себя, поэтому $\sum\limits_{k=1}^{p-1}k^{-1}\equiv \sum\limits_{k=1}^{p-1}k \equiv \frac{p(p-1)}{2}\equiv 0 \pmod {p}$, но $\not\equiv 0 \pmod {p^2}$, т.к. $\frac{p-1}{2}$ на $p$ не делится.

[Noct]

Padawan в сообщении #1229834 писал(а):

Sonic86 в сообщении #1229614 писал(а):

Кстати верен более общий факт: $\sum\limits_{k=1}^{p-1}k^{-1}\equiv 0\pmod {p^2}$.

Хм, $k\mapsto k^{-1}$ есть биекция $\mathbb Z/p\mathbb Z$ на себя (при простом $p>2$), поэтому $\sum\limits_{k=1}^{p-1}k^{-1}\equiv \sum\limits_{k=1}^{p-1}k \equiv \frac{p(p-1)}{2}\equiv 0 \pmod {p}$, но $\not\equiv 0 \pmod {p^2}$, т.к. $\frac{p-1}{2}$ на $p$ не делится.

Да но тут фишка именно в том что рассматривается не $\mathbb Z/p\mathbb Z$, а $\mathbb Z/p^2\mathbb Z$
А если совсем строго то не само кольцо, а только мультипликативная группа
Эта формула равносильно тому что числитель дроби $\sum\limits_{k=1}^{p-1} \frac{1}{k}$, делится на $p^2$

[Padawan]

Noct в сообщении #1229836 писал(а):

Да но тут фишка именно в том что рассматривается не $\mathbb Z/p\mathbb Z$, а $\mathbb Z/p^2\mathbb Z$

Тогда я не совсем понял, что такое $k^{-1}$. В $\mathbb Z/p^2\mathbb Z$ $k^{-1}$ определено (однозначно) только для $k$, взаимно простых с $p$. Это имеется ввиду?

-- Пн июн 26, 2017 22:52:17 --

Padawan в сообщении #1229834 писал(а):

$\sum\limits_{k=1}^{p-1}k^{-1}\equiv 0\pmod {p^2}$.

Покажите на примере, что имеется ввиду. Пусть $p=3$.

[Noct]

Странно, но для $p=3$, формула не верна, но для
$p=5$,
Рассмотрим: $1^{-1} + 2^{-1} + 3^{-1} + 4^{-1}$
Так как
$1 \cdot 1 \equiv 1 \pmod{25} $
$2 \cdot 13 \equiv 1 \pmod{25} $
$3 \cdot 17 \equiv 1 \pmod{25} $
$4 \cdot 19 \equiv 1 \pmod{25} $
то

$$1^{-1} + 2^{-1} + 3^{-1} + 4^{-1} \equiv 1 + 13 + 17 + 19 \equiv 50 \equiv 0 \pmod{25}$$

-- 27.06.2017, 01:13 --

Цитата:

Тогда я не совсем понял, что такое $k^{-1}$. В $\mathbb Z/p^2\mathbb Z$ $k^{-1}$ определено (однозначно) только для $k$, взаимно простых с $p$. Это имеется ввиду?

Тут ИМХО правильнее не $\mathbb Z/p^2\mathbb Z$, использовать а $U(\mathbb Z/p^2\mathbb Z)$, которое обозначает группу обратимых по модулю $p^2$ элементов и в ней разумеется обратный определен однозначно. И в ней находятся только те числа, которые взаимно просты с $p^2$, и их ровно $p^2 - p$ штук. Хотя возможно я что-то не понимаю.

[Cash]

Если $1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{p-1} =\frac AB$,
то
$\frac CD = \frac{1}{1(p-1)} + \frac{1}{2(p-2)} + \cdots + \frac{1}{(p-1)1} = \frac 1p\left(\frac 11+\frac 1{p-1}\right) +\frac 1p\left(\frac 12+\frac 1{p-2}\right) + \cdots + \frac 1p\left(\frac 1{p-1}+\frac 11\right) = \frac 2p \cdot \frac {A}{B}$
Осталось доказать, что $C$ делится на $p$. Действуйте аналогично предыдущему.